Cho mạch điện gồm hai điện trở R1 = 10 Ω, R2 = 30 Ω mắc song song vào mạch điện thì điện trở tương đương của mạch là bao nhiêu ôm? *
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
30 tháng 10 2021
\(R=R1+\left(\dfrac{R2.R3}{R2+R3}\right)=10+\left(\dfrac{20.30}{20+30}\right)=22\left(\Omega\right)\)
30 tháng 10 2021
Điện trở tương đương:
\(R_{tđ}=R_1+\dfrac{R_2\cdot R_3}{R_2+R_3}=10+\dfrac{20\cdot30}{20+30}=22\Omega\)
13 tháng 10 2021
Do mắc song song nên:
\(R_{tđ}=\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}}\)\(\Rightarrow1=\dfrac{1}{\dfrac{1}{3}+\dfrac{1}{R_2}}\)
\(\Rightarrow\dfrac{1}{3}+\dfrac{1}{R_2}=1\Rightarrow\dfrac{1}{R_2}=\dfrac{2}{3}\Rightarrow R_2=1,5\left(\Omega\right)\)
N
19 tháng 10 2021
Bạn tự vẽ sơ đồ nhé!
a. \(R=\dfrac{R1.R2}{R1+R2}=\dfrac{10.30}{10+30}=7,5\Omega\)
\(U=U1=U2=12V\)(R1//R2)
\(\left\{{}\begin{matrix}I=U:R=12:7,5=1,6A\\I1=U1:R1=12:10=1,2A\\I2=U2:R2=12:30=0,4A\end{matrix}\right.\)
\(S=\dfrac{p.l}{R}=\dfrac{1,1.10^{-6}.2}{30}=7,\left(3\right).10^{-8}m^2\)
\(\Rightarrow d=\sqrt{\dfrac{4S}{\pi}}=\sqrt{\dfrac{4.7,\left(3\right).10^{-8}}{\pi}}\simeq5,2.10^{-4}\simeq0,52mm^2\)
N
21 tháng 10 2021
a. \(R=\dfrac{R1.R2}{R1+R2}=\dfrac{10.30}{10+30}=7,5\Omega\)
b. \(U=U1=U2=12V\)(R1//R2)
\(\left\{{}\begin{matrix}I1=U1:R1=12:10=1,2A\\I2=U2:R2=12:30=0,4A\end{matrix}\right.\)
c. \(R=p\dfrac{l}{S}\Rightarrow S=\dfrac{p.l}{R}=\dfrac{1,1.10^{-6}.2}{30}=7,\left(3\right).10^{-8}\left(m^2\right)\)
\(S=\pi\dfrac{d^2}{4}\Rightarrow d^2=\dfrac{4S}{\pi}=\dfrac{4.7,\left(3\right).10^{-8}}{\pi}=2,675159236.10^{-7}\)
\(\Rightarrow d=\sqrt{2,675159236.10^{-7}}.1000=0,517220382\left(mm\right)\)
AN
2 tháng 10 2021
R12=\(\dfrac{R1.R2}{R1+R2}=\dfrac{20.100}{20+100}=\dfrac{50}{3}\)ôm
Rtđ=\(\dfrac{R12.R3}{R12+R3}=160ôm\)
19 tháng 9 2021
R1//R2//R3
a,\(\Rightarrow\dfrac{1}{RTt}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}\Rightarrow Rtd=12,5\Omega\)
b,\(\Rightarrow\left\{{}\begin{matrix}I1=\dfrac{37,5}{25}=1,5A\\I2=\dfrac{37,5}{50}=0,75A\\I3=\dfrac{37,5}{50}=0,75A\end{matrix}\right.\)\(\Rightarrow Im=\dfrac{37,5}{Rtd}=3A\)
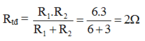
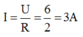
Điện trở tương đương của mạch:
Ta có: \(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Leftrightarrow R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{10.30}{10+30}=7,5\left(\Omega\right)\)