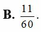Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Gọi số đó là \(\overline{ab}\)
a có 5 cách chọn (khác 0), b có 5 cách chọn (khác a)
Theo quy tắc nhân ta có: \(5.5=25\) số
b. Gọi số đó là \(\overline{abc}\)
a có 5 cách chọn (khác 0), b có 5 cách chọn (khác a), c có 4 cách chọn (khác a và b)
Có: \(5.5.4=100\) số
c. Gọi số đó là \(\overline{abcd}\)
Do số chẵn nên d chẵn
- TH1: \(d=0\) (1 cách chọn d)
a có 5 cách chọn (khác d), b có 4 cách chọn (khác a và d), c có 3 cách chọn
\(\Rightarrow1.5.4.3=60\) số
- TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (2 và 4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn (khác a và d), c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Theo quy tắc cộng, có: \(60+96=156\) số thỏa mãn
d.
Gọi số đó là \(\overline{abcde}\)
Số lẻ nên e lẻ \(\Rightarrow\) e có 3 cách chọn (1;3;5)
a có 4 cách chọn (khác 0 và e), b có 4 cách chọn (khác a và e), c có 3 cách, d có 2 cách
\(\Rightarrow3.4.4.3.2=288\) số
Đề bài chính xác là gì nhỉ? Lấy ra 3 số từ tập đã cho, tính xác suất để trong 3 số có đúng 1 số có chữ số 3?
Số cách lập số có 3 chữ số phân biệt từ tập đã cho: \(4.4.3=48\)
Lấy ra 3 số bất kì: có \(C_{48}^3\) cách
Gọi số có 3 chữ số khác nhau lập từ các số nói trên và luôn có mặt chữ số 3 là abc
TH1: a=3: bc có \(A_4^2=12\) cách chọn
TH2: a khác 3: chọn a có 3 cách, số còn lại có 3 cách, hoán vị nó với 3 cách 2 cách \(\Rightarrow3.3.2=18\) số
\(\Rightarrow12+18=30\) số có mặt chữ số 3 và 18 số không có mặt chữ số 3
Chọn 3 số trong đó có đúng 1 số có mặt chữ số 3: \(C_{30}^1.C_{18}^2\) cách
Xác suất: \(P=\dfrac{C_{30}^1C_{18}^2}{C_{48}^3}=...\)
Chọn đáp án B
Phương pháp
Chia các TH sau:
TH1: a<b<c.
TH2: a=b<c.
TH3: a<b=c.
TH4: a=b=c.
Cách giải
Gọi số tự nhiên có 3 chữ số là a b c ¯ (0≤a,b,c≤9, a≠0).
=> S có 9.10.10=900 phần tử. Chọn ngẫu nhiên một số từ S => n(Ω)=900
Gọi A là biến cố: “Số được chọn thỏa mãn a≤b≤c”.
TH1: a<b<c. Chọn 3 số trong 9 số từ 1 đến 9, có duy nhất một cách xếp chúng theo thứ tự tăng dần từ trái qua phải nên TH này có C 9 3 số thỏa mãn.
TH2: a=b<c, có C 9 2 số thỏa mãn.
TH3: a<b=c có C 9 2 số thỏa mãn.
TH4: a=b=c có 9 số thỏa mãn.
⇒ n ( A ) = C 9 3 + 2 C 9 2 + 9 = 165
Vậy P ( A ) = 11 60 .
