với giá trị nguyên nào của x thì biểu thức \(M=\frac{17-2x}{7-2x}\)có giá trị lớn nhất?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YN
30 tháng 6 2021
\(1.\)
\(-17-\left(x-3\right)^2\)
Ta có: \(\left(x-3\right)^2\ge0\)với \(\forall x\)
\(\Leftrightarrow-\left(x-3\right)^2\le0\)với \(\forall x\)
\(\Leftrightarrow17-\left(x-3\right)^2\le17\)với \(\forall x\)
Dấu '' = '' xảy ra khi:
\(\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Vậy \(Max=-17\)khi \(x=3\)
YN
30 tháng 6 2021
\(2.\)
\(A=x\left(x+1\right)+\frac{3}{2}\)
\(A=x^2+x+\frac{3}{2}\)
\(A=\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
\(\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
\(\Leftrightarrow\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
Vậy \(Max=\frac{5}{4}\)khi \(x=\frac{-1}{2}\)
CM
31 tháng 5 2017
Giá trị của biểu thức 2 x - 3 35 + x x - 2 7 không lớn hơn giá trị của biểu thức x 2 7 - 2 x - 3 5 nghĩa là 2 x - 3 35 + x x - 2 7 ≤ x 2 7 - 2 x - 3 5
Ta có:
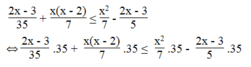
⇔ 2x – 3 + 5 x 2 – 10x ≤ 5 x 2 – 14x + 21
⇔ 2x + 5 x 2 – 10x – 5 x 2 + 14x ≤ 21 + 3
⇔ 6x ≤ 24
⇔ x ≤ 4
Vậy với x ≤ 4 thì giá trị của biểu thức 2 x - 3 35 + x x - 2 7 không lớn hơn giá trị của biểu thức x 2 7 - 2 x - 3 5
PT
1
AH
Akai Haruma
Giáo viên
29 tháng 1 2022
Lời giải:
Để $P=\frac{9-2x}{x-3}$ nguyên thì:
$9-2x\vdots x-3$
$\Leftrightarrow 3-2(x-3)\vdots x-3$
$\Leftrightarrow 3\vdots x-3$
Khi đo $x-3$ là ước của $3$
$\Leftrightarrow x-3\in\left\{\pm 1; \pm 3\right\}$
$\Leftrightarrow x\in \left\{4; 2; 6; 0\right\}$
I
3
24 tháng 10 2016
Với các giá trị của x sao cho \(2x-1\ne0\) thì \(\left|2x-1\right|>0\). Khi đó
\(A=5-\left|2x-1\right|< 5\)
Vớ giá trị của x mà \(2x-1=0\) thì \(\left|2x-1\right|=0\). Khi đó
\(A=5-0=5\)
Vậy, nếu \(2x-1=0\), tức là với \(x=\frac{1}{2}\) thì A đạt giá trị lớn nhất.
24 tháng 10 2016
Có: \(\left|2x-1\right|\ge0\forall x\) \(\Rightarrow-\left|2x-1\right|\le0\forall x\)
\(\Rightarrow5-\left|2x-1\right|\le5\forall x\)
Dấu ''='' xảy ra khi |2x - 1| = 0
=> 2x - 1 = 0
=> 2x = 1
=> \(x=\frac{1}{2}\)
Vậy với x = \(\frac{1}{2}\) thì biểu thức A có giá trị lớn nhất là 5
HN
17 tháng 1 2017
\(A=\frac{12-x}{4-x}=1+\frac{8}{4-x}\)
A nhận giá trị nguyên khi 4 - x là ước nguyên của 8. Mà để A lớn nhất thì 4 - x phải là ước nguyên dương bé nhất hay x - 4 = 1
<=> x = 5
Vậy GTNN của A là 1 + 8 = 9
M
2
5 tháng 11 2021
\(M=x^2+2x-8-x^3+x^3=x^2+2x-8=\left(x^2+2x+1\right)-9=\left(x+1\right)^2-9\ge-9\)
\(minM=-9\Leftrightarrow x=-1\)
5 tháng 11 2021
\(M=x^2+2x-8-x^3+x^3=\left(x^2+2x+1\right)-9=\left(x+1\right)^2-9\ge-9\\ M_{min}=-9\Leftrightarrow x=-1\)
22 tháng 2 2018
Để A đạt GTLN thì \(\frac{3}{4-x}\)phải đạt giá trị lớn nhất\(\Rightarrow\)4-x phải bé nhất và 4-x>0
\(\Rightarrow4-x=1\rightarrow x=3\)
thay vào ta đc A=3
B3
\(B=\frac{7-x}{4-x}=\frac{4-x+3}{4-x}=\frac{4-x}{4-x}+\frac{3}{4-x}\)\(=1+\frac{3}{4-x}\)
Để b đạt GTLn thì 3/4-x phải lớn nhất (làm tương tụ như bài 2 )
Vậy gtln của 3/4-x là 3 thay vào ta đc b=4
Lâm như bài 2 Gtln của\(\frac{3}{4-x}\)
22 tháng 2 2018
B1\(\frac{4x-3}{2x+1}=\frac{4x+2-5}{2x+1}=\frac{2.\left(2x+1\right)-5}{2x+1}\)\(=\frac{2.\left(2x+1\right)}{2x+1}-\frac{5}{2x+1}=2-\frac{5}{2x+1}\)
VÌ A\(\varepsilon Z\),2\(\varepsilon Z\)\(\Rightarrow\)\(\frac{5}{2x+1}\varepsilon Z\)\(\rightarrow2x+1\varepsilonƯ\left(5\right)\)={1;-1;5;-5}
\(\Rightarrow\)x={0;-1;23}
