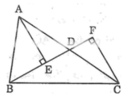
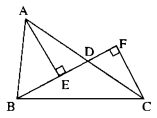
1 ) Cho tam giác ABC , D nằm giữa A và C sao cho BD không vuông góc với AC . Gọi E và F là chân các đường vuông góc vẽ từ A và C đến đường thẳng BD . So sánh AD với tổng AE + CF
2 ) Cho tam giác ABC vuông tại A , M là trung điểm của AC . Gọi E và F là chân các đường vuông góc vẽ từ A và C đến đường thẳng BM . Chứng minh rằng : AB < BE + BF / 2