a) Cho đa thức f(x)= x4-3x3+bx2+ax+b
g(x)= x2-1
Tìm các hệ số của a,b để f(x) chia hết cho g( x)
b) Tìm giá trị nhỏ nhất của biểu thức A= x(2x-3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 11 2022
a: f(x) chiahết cho g(x)
=>\(x^4-x^2-3x^3+3x+\left(b+1\right)x^2-\left(b+1\right)+\left(a-3\right)x+2b+1⋮x^2-1\)
=>a-3=0 và 2b+1=0
=>a=3 và b=-1/2
b: A=2x^2-3x
=2(x^2-3/2x)
=2(x^2-2*x*3/4+9/16-9/16)
=2(x-3/4)^2-9/8>=-9/8
Dấu = xảy ra khi x=3/4
24 tháng 10 2021
\(f\left(x\right)⋮g\left(x\right)\)
\(\Leftrightarrow x^4-3x^3+4x^2-x^2+3x-4+\left(a-3\right)x+\left(b+4\right)⋮x^2-3x+4\)
\(\Leftrightarrow\left(a,b\right)=\left(3;-4\right)\)
HH
14 tháng 8 2017
My Nguyễn ơi,bạn truy cập vào đường link này để tìm câu hỏi tương tự của câu a/Bài 1 nhé
https://vn.answers.yahoo.com/question/index?qid=20110206184834AAokV5m&sort=N
CM
21 tháng 10 2017
Ta có
Phần dư của phép chia f(x) cho g(x) là R = (a – 1)x + b + 30
Để phép chia trên là phép chia hết thì R = 0 với mọi x
ó (a – 1)x + b + 30 = 0 với mọi x
ó a - 1 = 0 b + 30 = 0 ó a = 1 b = - 30
Vậy a = 1; b = -30
Đáp án cần chọn là: D
CM
18 tháng 12 2017
Ta có
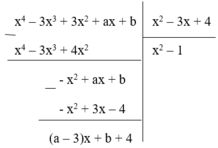
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó a - 3 = 0 b + 4 = 0
ó a = 3 b = - 4 => ab = -12
Đáp án cần chọn là: A
Z2
1
a: \(\Leftrightarrow x^4-x^2-3x^3+6x+\left(b+1\right)x^2-b-1+\left(a-6\right)x+2b+1⋮x^2-1\)
=>a-6=0 và 2b+1=0
=>a=6; b=-1/2
b: =2x^2-3x
=2(x^2-3/2x)
=2(x^2-2*x*3/4+9/16-9/16)
=2(x-3/4)^2-9/8>=-9/8
Dấu = xảy ra khi x=3/4