Bài 5: Tìm GTNN của các biểu thức sau:
a) A = x^2 – 4x + 9
b) B = x^2 – x + 1
c) C = 2x^2 – 6x
Bài 4: Tìm GTLN của các đa thức:
a) M = 4x – x^2 + 3
b) N = x – x^2
c) P = 2x – 2x^2 – 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: M=−x2−2x+5
=−(x2+2x−5)
=−(x2+2x+1)+6
=−(x+1)2+6
Vì −(x+1)2≤0∀x
⇒−(x+1)2+6≤6∀x
Dấu "=" xảy ra ⇔
Vậy
Đặt A=4x−x2+3
=−x2+4x+3=−(x2−4x−3)
=−(x2−4x+4−7)
=−[(x−2)2−7]
=−(x−2)2+7
Ta có: −(x−2)2≤0⇒−(x−2)2+7≤7
Dấu " = " khi (x−2)2=0⇔x=2
Vậy MAXA=7 khi x = 2

Ta có : P = x2 - 2x + 5 = x2 - 2x + 1 + 4 = (x - 1)2 + 4
Vì \(\left(x-1\right)^2\ge0\forall x\)
Suy ra : \(P=\left(x-1\right)^2+4\ge4\forall x\)
Nên : Pmin = 4 khi x = 1
b) Ta có Q = 2x2 - 6x = 2(x2 - 3x) = 2(x2 - 3x + \(\frac{9}{4}-\frac{9}{4}\) ) = \(2\left(x^2-3x+\frac{9}{4}\right)-\frac{9}{2}=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\)
Vì \(2\left(x-\frac{3}{2}\right)^2\ge0\forall x\)
SUy ra ; \(Q=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)
Vậy \(Q_{min}=-\frac{9}{2}\) khi \(x=\frac{3}{2}\)

Bài 2 :
a, \(x^2-4x+4+1=\left(x-2\right)^2+1\ge1\)
Dấu ''='' xảy ra khi x = 2
b, Ta có \(\left(x+1\right)^2+10\ge10\Rightarrow\dfrac{-100}{\left(x+1\right)^2+10}\ge-\dfrac{100}{10}=-10\)
Dấu ''='' xảy ra khi x = -1
Bài 1 :
a, Ta có \(A\left(x\right)=x^2-4x+4=0\Leftrightarrow\left(x-2\right)^2=0\Leftrightarrow x=2\)
b, \(B\left(x\right)=x^2\left(2x+1\right)+\left(2x+1\right)=\left(x^2+1>0\right)\left(2x+1\right)=0\Leftrightarrow x=-\dfrac{1}{2}\)
c, \(C\left(x\right)=\left|2x-3\right|=\dfrac{1}{3}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{1}{3}+3=\dfrac{10}{3}\\2x=-\dfrac{1}{3}+3=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)

a: Ta có: \(A=-x^2+4x+3\)
\(=-\left(x^2-4x+4-7\right)\)
\(=-\left(x-2\right)^2+7\le7\forall x\)
Dấu '=' xảy ra khi x=2
b: Ta có: \(B=-x^2+x\)
\(=-\left(x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

Thật ra cách làm dạng bài này cũng gần giống như bài tìm gtnn bạn vừa hỏi, chỉ khác ở chỗ đặt dấu âm ra ngoài để tìm được gtln thôi.

a: Khi x=2/3 thì \(A=\dfrac{\dfrac{2}{3}-2}{\dfrac{2}{3}}=\dfrac{-4}{3}\cdot\dfrac{3}{2}=-2\)
b: \(B=\dfrac{4x}{x+1}-\dfrac{x}{x-1}+\dfrac{2x}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{4x^2-4x-x^2-x+2x}{\left(x-1\right)\left(x+1\right)}=\dfrac{3x^2-3x}{\left(x-1\right)\left(x+1\right)}=\dfrac{3x}{x+1}\)
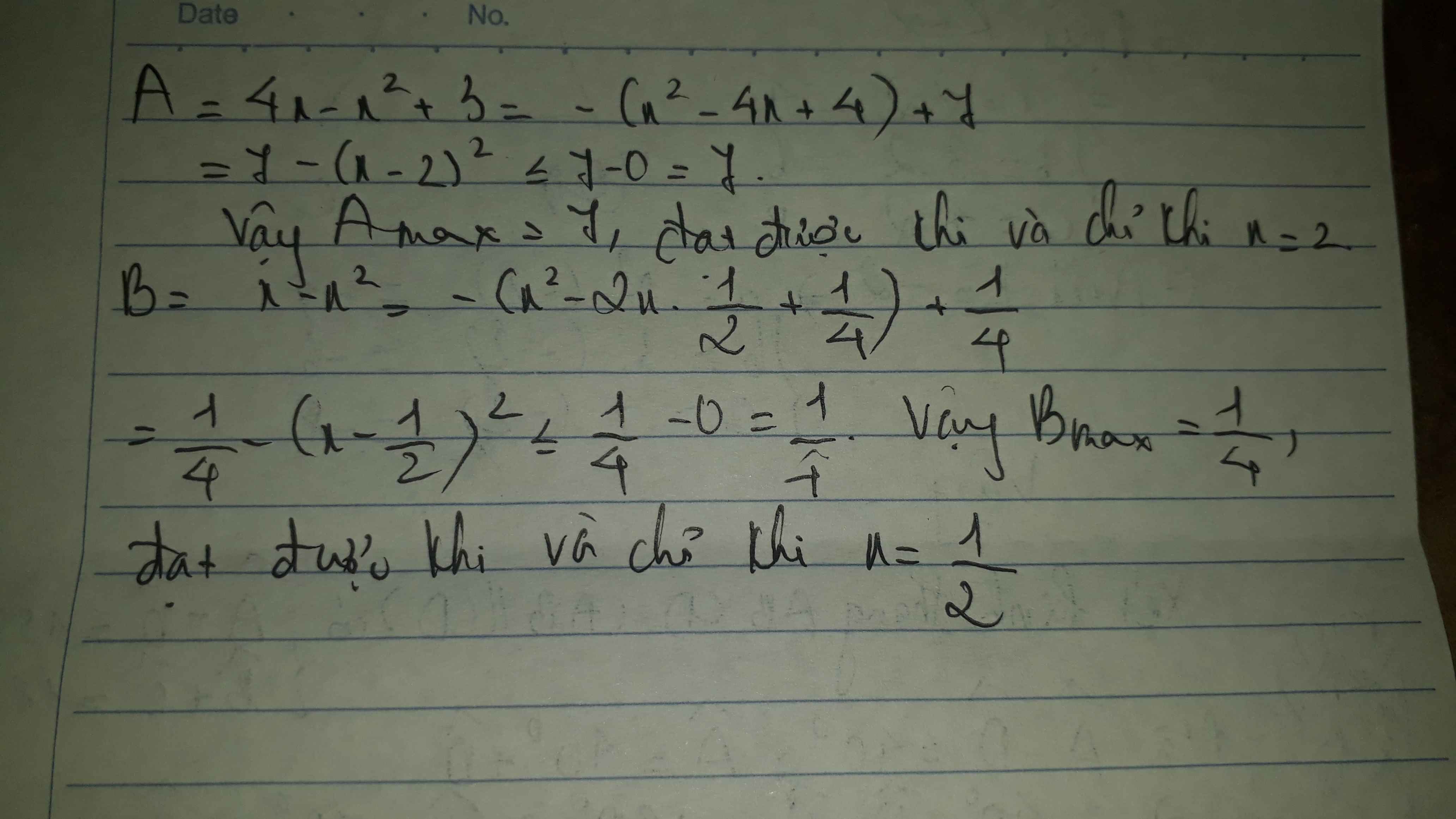

Bài 5:
a) \(A=x^2-4x+9=\left(x^2-4x+4\right)+5=\left(x-2\right)^2+5\ge5\)
\(minA=5\Leftrightarrow x=2\)
b) \(B=x^2-x+1=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(minB=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=2x^2-6x=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
\(minC=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{3}{2}\)
Bài 4:
a) \(M=4x-x^2+3=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
\(maxM=7\Leftrightarrow x=2\)
b) \(N=x-x^2=-\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
\(maxN=\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(P=2x-2x^2-5=-2\left(x^2-x+\dfrac{1}{4}\right)-\dfrac{9}{2}=-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{2}\le-\dfrac{9}{2}\)
\(maxP=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{1}{2}\)