Tìm x để M<4 biết M=\(\frac{4x-1}{x^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 3 2022
a: Để M có nghĩa thì x+2<>0
hay x<>-2
b: Để M=4 thì 4x+8=3x+9
hay x=1(nhận)
c: Để M là số nguyên thì \(3x+9⋮x+2\)
\(\Leftrightarrow3x+6+3⋮x+2\)
\(\Leftrightarrow x+2\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{-1;-3;1;-5\right\}\)
DA
8 tháng 3 2022
`a)`
Để `M` có nghĩa thì:
`x+2\ne0`
`<=>x\ne-2`
Vậy `x\ne-2` thì `M` có nghĩa
`b)`
`M=4`
`<=>(3x+9)/(x+2)=4`
`=>4x+8=3x+9`
`<=>4x-3x=9-8`
`<=>x=1`
Vậy `x=1` thì `M=4`
`c)`
`M\inZZ<=>(3x+9)/(x+2)\inZZ`
`=>3x+9\vdotsx+2`
`=>3x+6+3\vdotsx+2`
`=>3.(x+2)+3\vdotsx+2`
`=>x+2\in Ư(3)={+-1;+-3}`
Ta có bảng:
$\begin{array}{|c|c|}\hline x+2&1&-1&3&-3\\\hline x&-1&-3&1&-5\\\hline\end{array}$
Vậy `x\in{-1;-3;1;-5}` thì `M\inZZ`
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
ĐKXĐ: \(x\ge0\)
\(\left(x^2-x-m\right)\sqrt{x}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-x-m=0\left(1\right)\end{matrix}\right.\)
Giả sử (1) có nghiệm thì theo Viet ta có \(x_1+x_2=1>0\Rightarrow\left(1\right)\) luôn có ít nhất 1 nghiệm dương nếu có nghiệm
Do đó:
a. Để pt có 1 nghiệm \(\Leftrightarrow\left(1\right)\) vô nghiệm
\(\Leftrightarrow\Delta=1+4m< 0\Leftrightarrow m< -\dfrac{1}{4}\)
b. Để pt có 2 nghiệm pb
TH1: (1) có 1 nghiệm dương và 1 nghiệm bằng 0
\(\Leftrightarrow m=0\)
TH2: (1) có 2 nghiệm trái dấu
\(\Leftrightarrow x_1x_2=-m< 0\Leftrightarrow m>0\)
\(\Rightarrow m\ge0\)
c. Để pt có 3 nghiệm pb \(\Leftrightarrow\) (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=1+4m>0\\x_1x_2=-m>0\\\end{matrix}\right.\) \(\Leftrightarrow-\dfrac{1}{4}< m< 0\)
4 tháng 3 2023
a: =>m^2x-m^3-x+3m-2=0
=>x(m^2-1)=m^3-3m+2
=>x(m-1)(m+1)=m^3-m-2m+2=m(m-1)(m+1)-2(m-1)=(m-1)^2*(m+2)
Để đây là pt bậc nhất 1 ẩn thì (m-1)(m+1)<>0
=>m<>1 và m<>-1
b: Khi m=0 thì pt sẽ là x+2=0
=>x=-2
c: Khi x=3 thì pt sẽ là:
3(m^2-1)=m^3-3m+2
=>(m-1)^2(m+1)-3(m-1)(m+1)=0
=>(m-1)(m+1)(m-1-3)=0
=>(m-1)(m+1)(m-4)=0
=>\(m\in\left\{1;-1;4\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
\(\Delta'=\left(m-2\right)^2-3\left(m-2\right)=\left(m-2\right)\left(m-5\right)\)
a.
Phương trình có nghiệm kép khi:
\(\left\{{}\begin{matrix}a=m-2\ne0\\\Delta'=\left(m-2\right)\left(m-5\right)=0\end{matrix}\right.\) \(\Rightarrow m=5\)
b.
Phương trình có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m-2\ne0\\\left(m-2\right)\left(m-5\right)>0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m>5\\m< 2\end{matrix}\right.\)
c.
- Với \(m=2\) pt vô nghiệm
- Với \(m\ne2\) pt có nghiệm khi: \(\left(m-2\right)\left(m-5\right)\ge0\)
\(\Rightarrow\left[{}\begin{matrix}m\ge5\\m< 2\end{matrix}\right.\)
d.
Pt vô nghiệm khi: \(\left[{}\begin{matrix}m=2\\\left(m-2\right)\left(m-5\right)< 0\end{matrix}\right.\)
\(\Rightarrow2\le m< 5\)
9 tháng 10 2021
a) ĐKXĐ: \(x\ge0,x\ne9\)
\(A=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3}{\sqrt{x}+3}\)
b) \(A=\dfrac{3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{64}+3}=\dfrac{3}{8+3}=\dfrac{3}{11}\)
c) \(2A=\dfrac{6}{\sqrt{x}+3}=1\Rightarrow\sqrt{x}+3=6\Rightarrow x=9\left(tm\right)\)
g) \(A=\dfrac{3}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}+3\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{0\right\}\)
h) \(A=\dfrac{3}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}+3\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{0\right\}\)
k) \(2A=\dfrac{6}{\sqrt{x}+3}=m\)
BA
21 tháng 3 2021
a, Với m=1 thay vào pt
Ta có
\(x^2+x-1=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{-1+\sqrt{5}}{2}\\x=\dfrac{-1-\sqrt{5}}{2}\end{matrix}\right.\)
b,
Thay x=2 vào pt
ta có
\(4-2-3m+2=0\)
\(\Leftrightarrow4-3m=0\)
\(\Rightarrow m=\dfrac{4}{3}\)
c, Ta có
\(\Delta=1-4\left(-3m+2\right)\)
\(=12m-7\)
Để pt có 2 nghiệm phân biệt thì \(\Delta>0\)
\(\Rightarrow12m-7>0\)
\(\Rightarrow m>\dfrac{7}{12}\)
d,
Để ptcos nghiệm kép thì \(\Delta=0\)
\(\Rightarrow12m-7=0\)
\(\Rightarrow m=\dfrac{7}{12}\)
e,
Để pt vô nghiệm thì \(\Delta< 0\)
\(\Rightarrow m< \dfrac{7}{12}\)
Y
10 tháng 3 2023
\(f\left(x\right)=\left(m-4\right)x^2+\left(m+1\right)x+2m-1\)
\(f\left(x\right)< 0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a< 0\\\Delta< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-4< 0\\\left(m+1\right)^2-4\left(m-4\right)\left(2m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 4\\m^2+2m+1-4\left(2m^2-m-8m+4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow m^2+2m+1-8m^2+36m-16< 0\)
\(\Leftrightarrow-7m^2+38m-15< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 4\\\left[{}\begin{matrix}m< \dfrac{3}{7}\\m>5\end{matrix}\right.\end{matrix}\right.\)
\(KL:m\in\left(5;+\infty\right)\)
20 tháng 12 2022
a: Thay x=1 và y=3 vào (d), ta đc:
m-1+2=3
=>m+1=3
=>m=2
b: Thay y=0 vào (d), ta đc:
x-1=0
=>x=1
Thay x=1 và y=0 vào (d1), ta được:
2*1+m-1=0
=>m=-1
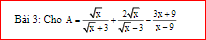
\(\frac{4x-1}{x^2}< 4\)
\(\Leftrightarrow\)\(4x^2>4x-1\)
\(\Leftrightarrow\)\(4x^2-4x+1>0\)
\(\Leftrightarrow\)\(\left(2x-1\right)^2>0\)
Mà \(\left(2x-1\right)^2\ge0\) nên để \(\left(2x-1\right)^2>0\) thì \(2x-1\ne0\)\(\Leftrightarrow\)\(x\ne\frac{1}{2}\)
Vậy để \(M< 4\) thì \(x\ne\frac{1}{2}\)
Chúc bạn học tốt ~