Mình cần gấp lắm ạ 😓. Cảm ơn trước !!!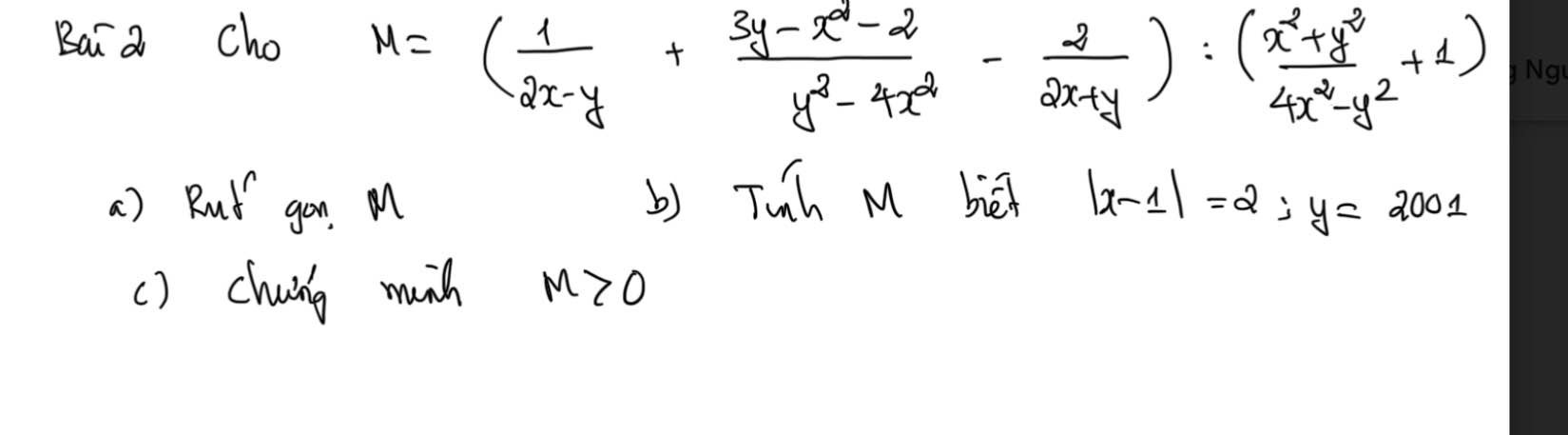
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d) Gọi x,y lần lượt là số mol Al, Fe
\(\left\{{}\begin{matrix}27x+56y=8,3\\1,5x+y=0,25\end{matrix}\right.\)
=> x=0,1 ; y=0,1
Kết tủa : Al(OH)3, Fe(OH)2
Bảo toàn nguyên tố Al: \(n_{Al\left(OH\right)_3}=n_{Al}=0,1\left(mol\right)\)
Bảo toàn nguyên tố Fe: \(n_{Fe\left(OH\right)_2}=n_{Fe}=0,1\left(mol\right)\)
=> \(m=0,1.78+0,1.90=16,8\left(g\right)\)
Nung kết tủa thu được chất rắn : Al2O3 và FeO
Bảo toàn nguyên tố Al: \(n_{Al_2O_3}.2=n_{Al}\Rightarrow n_{Al_2O_3}=0,05\left(mol\right)\)
Bảo toàn nguyên tố Fe: \(n_{FeO}=n_{Fe}=0,1\left(mol\right)\)
=> \(a=0,05.102+0,1.72=12,3\left(g\right)\)

ảnh cung xử nữ đây nha bạn mẹ mình cung xử nữ nẹ mình sinh lắm luôn ý mình thì cung sư tử nha mình sinh ngày 10/8/2010 mha



Bài 3 :
Đổi : s= 2300m = 2,3 km
Nam đến trường lúc : 7h - 8 phút = 6h52ph
Tổng thời gian Nam đã đi là :t = 6h52ph - 6h25ph = 27ph = 0.45h
Vận tốc của Nam là : v = \(\dfrac{s}{t}\) = \(\dfrac{2.3}{0.45}\) = \(\dfrac{46}{9}\)( km/h )
đổi ra m/s thì bằng \(\dfrac{46}{9}\) : 3,6 =1.41 m/s
bài 4 :
Vận tốc của vận động viên chạy là : v = \(\dfrac{S}{t}\) = \(\dfrac{100}{9.85}\) = 10,15 (m/s) = 36,54 km/h
so sánh 36 km/h > 36.54 km/h => vận động viên chạy nhanh hơn xe máy

(a) \(A=\dfrac{3}{x-2}\in Z\)
\(\Rightarrow\left(x-2\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\\x=4\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{-2;0;2;4\right\}.\)
(b) \(B=-\dfrac{11}{2x-3}\in Z\)
\(\Rightarrow\left(2x-3\right)\inƯ\left(11\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=1\\2x-3=-1\\2x-3=11\\2x-3=-11\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=7\\x=-4\end{matrix}\right.\)
Vậy: \(x\in\left\{-4;1;2;7\right\}.\)
(c) \(C=\dfrac{x+3}{x+1}=\dfrac{\left(x+1\right)+2}{x+1}=1+\dfrac{2}{x+1}\in Z\Rightarrow\dfrac{2}{x+1}\in Z\)
\(\Rightarrow\left(x+1\right)\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x+1=1\\x+1=-1\\x+1=2\\x+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=1\\x=-3\end{matrix}\right.\)
Vậy: \(x\in\left\{-3;-2;0;1\right\}.\)
(d) \(D=\dfrac{2x+10}{x+3}=\dfrac{2\left(x+3\right)+4}{x+3}=2+\dfrac{4}{x+3}\in Z\Rightarrow\dfrac{4}{x+3}\in Z\)
\(\Rightarrow\left(x+3\right)\inƯ\left(4\right)=\left\{\pm1;\pm2\pm4\right\}\)
\(\Rightarrow x\in\left\{-2;-4;-1;-5;1;-7\right\}\)

a: \(=27\cdot25-25\cdot127=25\cdot\left(27-127\right)=25\cdot\left(-100\right)=-2500\)
b: \(=\dfrac{-5}{12}+\dfrac{9}{12}-\dfrac{4}{12}=0\)
c: \(=\dfrac{5}{9}\left(\dfrac{7}{13}+\dfrac{9}{13}-\dfrac{3}{13}\right)=\dfrac{5}{9}\)

Gọi tam giác ABC vuông tại A, trung tuyến AM, đường cao AH
\(\Rightarrow AM=5\left(cm\right);AH=4\left(cm\right)\)
Ta có AM là trung tuyến ứng với cạnh huyền BC
\(\Rightarrow BC=2AM=10\left(cm\right)\)
Áp dụng HTL tam giác \(AH\cdot BC=AB\cdot AC\Rightarrow AB\cdot AC=40\Rightarrow AB=\dfrac{40}{AC}\\ \dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\\ \Rightarrow\dfrac{1}{16}=\dfrac{1}{\dfrac{1600}{AC^2}}+\dfrac{1}{AC^2}\\ \Rightarrow\dfrac{AC^4+1600}{1600AC^2}=\dfrac{100AC^2}{1600AC^2}\Rightarrow AC^4-100AC^2+1600=0\\ \Rightarrow\left(AC^2-80\right)\left(AC^2-20\right)=0\\ \Rightarrow\left[{}\begin{matrix}AC^2=80\\AC^2=20\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}AC=4\sqrt{5}\left(AC>0\right)\\AC=2\sqrt{5}\left(AC>0\right)\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}AB=2\sqrt{5}\\AB=4\sqrt{5}\end{matrix}\right.\)
Vậy với AB là cạnh góc vuông lớn thì \(\left(AB;AC;BC\right)=\left(4\sqrt{5};2\sqrt{5};10\right)\)

Câu 1:
a,MCD: R1//R2
\(R_{12}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{30\cdot20}{30+20}=12\left(\Omega\right)\)
b, MCD: R3nt(R1//R2)
\(R_{tđ}=R_3+R_{12}=30+12=42\left(\Omega\right)\)
Câu 2
a Điện trở và cường độ dòng điện tối đa mà biến trở đó có thể có
b,\(S=\dfrac{l\cdot\rho}{R}=\dfrac{100\cdot1,1\cdot10^{-6}}{200}=5,5\cdot10^{-7}\)
\(R=\sqrt{\dfrac{S}{\pi}}=\sqrt{\dfrac{5,5\cdot10^{-7}}{\pi}}=4,18\cdot10^{-4}\left(m\right)=0,418\left(mm\right)\)

\(x\times4+\frac{1}{2}\times x=55,35\)
\(\Leftrightarrow x\times\left(4+\frac{1}{2}\right)=55,35\)
\(\Leftrightarrow x\times4,5=55,35\)
\(\Leftrightarrow x=55,35:4,5\)
\(\Leftrightarrow x=12,3\)
Vậy x= 12,3
x.4+1/2.x=55,35
x.(4+1/2)=55.35
x.9/2=55,35
x=55,35:9/2
x=12,3
vì là máy ko có dấu nhân nên thay dấu nhân là dấu chấm


 đây nhé
đây nhé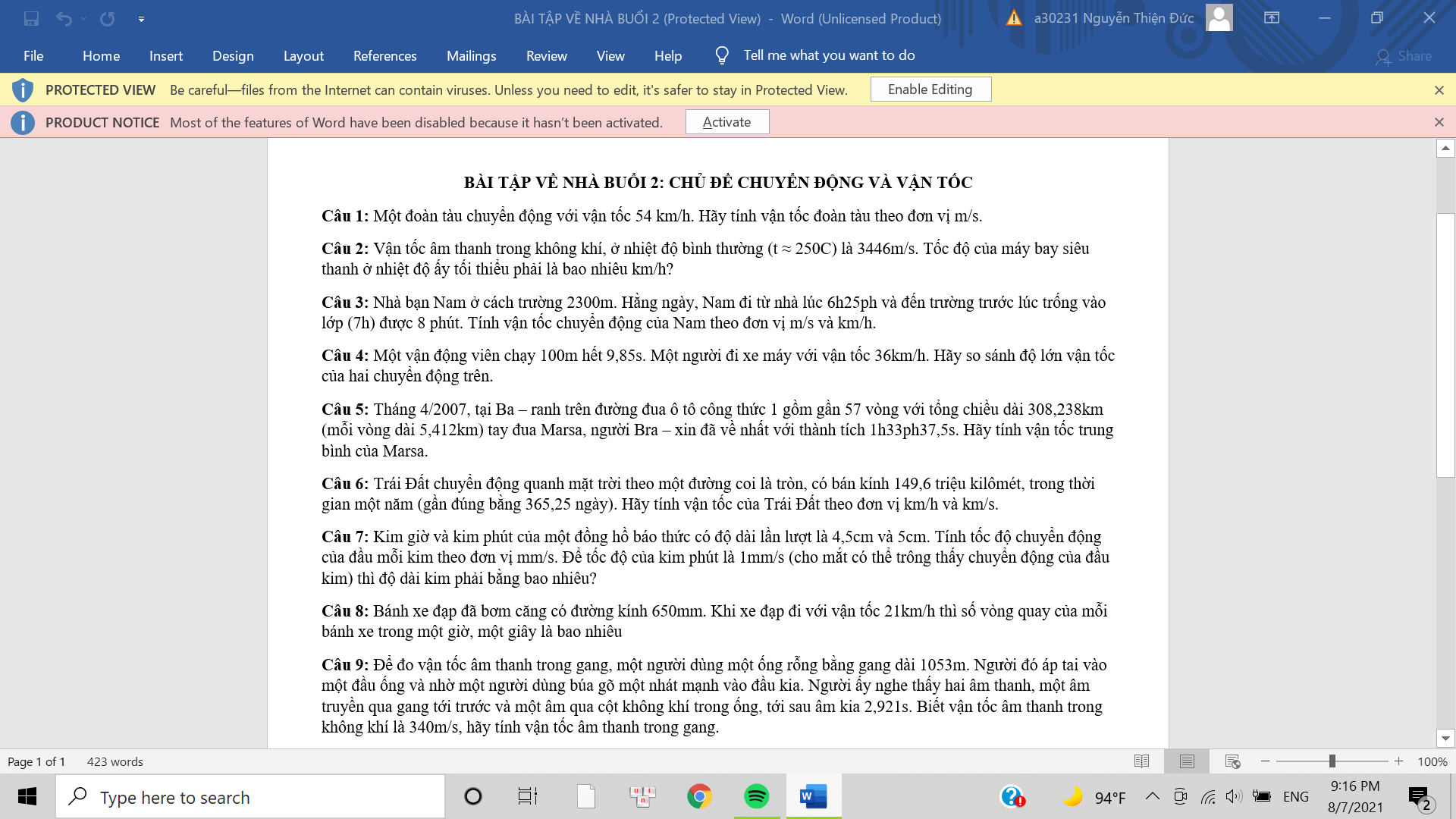
 giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước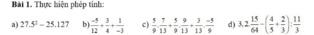


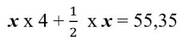
a: Ta có: \(M=\left(\dfrac{1}{2x-y}-\dfrac{-x^2+3y-2}{4x^2-y^2}-\dfrac{2}{2x+y}\right):\left(\dfrac{x^2+y^2}{4x^2-y^2}+1\right)\)
\(=\dfrac{2x+y+x^2-3y+2-4x+2y}{\left(2x-y\right)\left(2x+y\right)}:\dfrac{x^2+y^2+4x^2-y^2}{\left(2x-y\right)\left(2x+y\right)}\)
\(=\dfrac{x^2-2x+2}{5x^2}\)
c: Ta có: \(\left\{{}\begin{matrix}x^2-2x+2=\left(x-1\right)^2+1>0\forall x\\5x^2>0\forall xtmĐKXĐ\end{matrix}\right.\)
Do đó: M>0