3. Làm cách nào kiểm tra các số số nguyên tố bé hơn 100 trong bảng số dưới đây, nếu không cần học thuộc.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 1 2018
Giải : Cho n < 10000 ( n > 1 ) . Nếu n chia hết cho một số k nào đó ( 1 < k < n ) thì n là hợp số . Nếu n không chia hết cho mọi số nguyên tố p ( p2 \(\le\)n ) thì n là số nguyên tố .
Số 259 chia hết cho 7 nên là hợp số .
Số 353 không chia hết cho tất cả các số nguyên tố p mà p2 \(\le\)353 ( đó là các số nguyên tố 2 , 3 , 5 , 7 , 11 , 13 , 17 ) nên 353 là số nguyên tố .
8 tháng 10 2021
\(Số\) \(hạt\)\(không\) \(mang\) \(điện\) \(nhiều\) \(hơn\) \(số\) \(hạt\) \(mang\) \(điện\) \(dương\) \(là\) \(1hạt\).
\(\Rightarrow n-p=1\) \(\left(1\right)\)
\(Mà\) \(e+p+n=40\) \(\Leftrightarrow2p+n=40\) \(\left(e=p\right)\) \(\left(2\right)\)
\(Từ\) \(\left(1\right)và\left(2\right)\)\(\Rightarrow\) \(2p+n-n-p=40-1\)
\(\Rightarrow\) \(3p=39\)
\(\Rightarrow\) \(p=13\)
\(\Rightarrow\) \(n=13+1=14\)
\(Vậy\) \(p\) \(của\) \(A=13\) \(n=14\)
\(Nguyên\) \(tử\) \(A\) \(là\) \(NTHH\) \(Nhôm\) \(\left(Al\right)\)
B
4 tháng 10 2021
ta có 2p+n=40
-p+n=1
=>p=e=13
=>n=14 hạt
=>A là nhôm , Al (em tự tra bảng nếu cần biết thêm ha)
20 tháng 2 2023
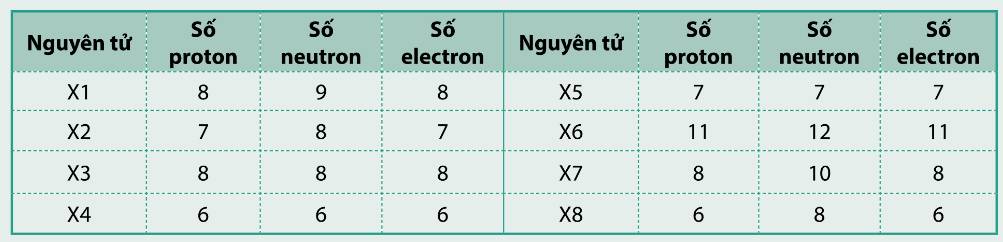
Các nguyên tố thuộc cùng `1` nguyên tố hóa học: `X1 - X3 - X7 , X2 - X5 , X4 - X8`
AH
Akai Haruma
Giáo viên
15 tháng 10 2021
Lời giải:
$89$ là số nguyên tố
$97$ là số nguyên tố
$125$ là hợp số, do $>5$ mà lại chia hết cho $5$
$2013$ là hợp số, do $>3$ mà lại chia hết cho $3$
$2018$ là hợp số, do $>2$ mà lại chia hết cho $2$
Tham khảo: Một số chứng minh về tính duy nhất của phân tích nguyên tố được dựa trên bổ đề Euclid: Nếu \(p\) là số nguyên tố và \(p\) chia hết một tích \(ab\) với \(a\) và \(b\) là số nguyên thì \(p\) cũng chia hết \(a\) hoặc \(b\) (hoặc cả hai). Ngược lại, nếu một số \(p\) có tính chất khi chia hết một tích thì nó cũng chia hết ít nhất một thừa số trong tích, thì \(p\) phải là số nguyên tố.
Nguồn: https://vi.wikipedia.org/wiki/S%E1%BB%91_nguy%C3%AAn_t%E1%BB%91