Cho ΔABC vuông tại A,đường cao AH.Gọi E,F lần lượt là hình chiếu của H lên AC,AB biết AB=6cm, AC =8cm
a)Chứng minh: AE.AC=AF.AB
b)Tính EF?
c)Chứng minh ΔAEF đồng dạng với ΔABC
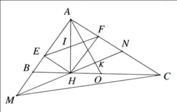
d)Gọi M,N lần lượt là trung điểm của BH,HC. O là giao điểm của AH và FE.Chứng minh ΔMON vuông
-GIÚP MÌNH VỚI Ạ-gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 10 2022
a: \(AE\cdot AC=AH^2\)
\(AF\cdot AB=AH^2\)
Do đó: AE*AC=AF*AB
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(AH=\dfrac{6\cdot8}{10}=4.8\left(cm\right)\)
Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
=>AH=EF=4,8cm
c: Ta có: AF*AB=AE*AC
nên AF/AC=AE/AB
Xét ΔAFE vuông tại A và ΔACB vuông tại A có
AF/AC=AE/AB
Do đó: ΔAFE đồng dạng với ΔACB
15 tháng 12 2022
a: BC=10cm
=>AD=5cm
b: Xet ΔABC có BE/BA=BD/BC
nên ED//AC và ED=AC/2=4cm
=>ED//AF và ED=AF
=>AEDF là hình bình hành
mà góc FAE=90 độ
nên AEDF là hình chữ nhật
c: Xét tứ giá ADBM có
E là trung điểm chung của AB và DM
DA=DB
Do dó: ADBM là hình thoi
\(C_{ADBM}=5\cdot4=20\left(cm\right)\)
d: Để AEDF là hình vuông thì AE=AF
=>AB=AC
12 tháng 11 2021
a: \(\widehat{C}=30^0\)
AB=4cm
\(AC=4\sqrt{3}\left(cm\right)\)
16 tháng 11 2021
\(\widehat{BHD}=\widehat{HAB}\)
\(\widehat{HAB}=\widehat{ADE}\)
Do đó: \(\widehat{ADE}=\widehat{BHD}\)
1 tháng 9 2021
a) Xét tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2\)(Định lý Pytago)
\(\Rightarrow AC^2=BC^2-AB^2=10^2-6^2=64\Rightarrow AC=8\left(cm\right)\)
Xét tam giác ABC vuông tại A có đường cao AH
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}=\dfrac{25}{576}\Rightarrow AH=\dfrac{24}{5}\left(cm\right)\)
Xét tứ giác AEHF có:
\(\widehat{AEH}=\widehat{EAF}=\widehat{AFH}=90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> \(EF=AH=\dfrac{24}{5}\left(cm\right)\)
b) Áp dụng tỉ số lượng giác của góc nhọn trong tam giác ABH và tam giác AHC vuông tại H:
\(AH^2=AE.AB\)
\(AH^2=AF.AC\)
\(\Rightarrow AE.AB=AF.AC\)
26 tháng 8 2022
Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)
a: \(AE\cdot AC=AH^2\)
\(AF\cdot AB=AH^2\)
Do đó: AE*AC=AF*AB
=>AE/AB=AF/AC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(AH=\dfrac{6\cdot8}{10}=4.8\left(cm\right)\)
Xét tứ giác ADHE có góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
=>AH=DE=4,8cm
c: Xét ΔAEFvuông tại A và ΔABC vuông tại A có
AE/AB=AF/AC
Do đó: ΔAEF đồng dạng với ΔABC