Hai người đứng ở một bên bờ sông cách nhau 250m cùng nhìn thấy một cù lao trên sông với các góc nâng lần lượt là 30 độ và 40 độ. Tính khoảng cách d từ bờ sông đến cù lao. (Vẽ thành hình tam giác. BC là bờ sông , AH là khoảng cách từ bờ sông đến cù lao)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 4 2020
THEO ĐỊNH LÝ EULER THÌ ĐỒ THỊ TRÊN CÓ NHIỀU HƠN 2 ĐỈNH LẺ NÊN KO CÓ ĐƯỜNG ĐI CÁC CÂY CẦU MÀ KO LẶP LẠI THẾ CHẲNG NHẼ LẠI KO CÓ CÁCH NÀO CHĂNG ? CHƯA HẲN ĐÂU ! NẾU CHÚNG MÌNH QUAN SÁT KĨ THÌ TA CÓ THỂ THẤY CÓ VÀI CHIẾC THYỀN VÌ VẬY TA CÓ THỂ SỬ DỤNG CÁC CON THUYỀN ĐỂ ĐI QUA CÁC CÂY CẦU MÀ KO LẶP LẠI
CM
2 tháng 3 2019
Chọn đáp án C
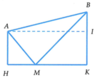
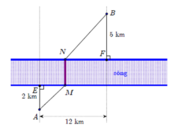
Khoảng cách từ A đến bờ sông là A H = 118 m ; khoảng cách từ B đến bờ sông là B K = 487 m (hình vẽ).
ta có
⇒ H K = 492 m .
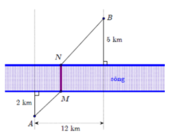
Người đó đi từ A đến vị trí M trên bờ sông để lấy nước, sau đó mang về B.
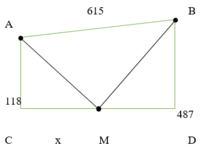
Đoạn đường người đó đi được là
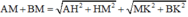
Đạo hàm
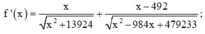
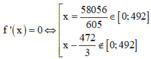
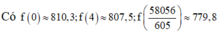
Vậy đoạn đường ngắn nhất người đó có thể đi là ≈ 779 , 8 m
CM
15 tháng 7 2019
Đáp án C
Cách 1: Giải bằng hàm số
Đặt CM = x (x > 0)
Dễ tính ra CD 
Từ đề bài ta có: f (x) = 
Quãng đường ngắn nhất người đó có thể đi
⇔ Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) =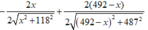 
=> f’(x) = 0
Ta có bảng biến thiên
| x |
0 |
0 |
492 |
| y’ |
|
+ 0 - |
|
| y |
779,8 |
||
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
⇔ AM + MB ngắn nhất
⇔ AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
⇔ AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng
8 tháng 10 2021
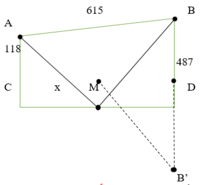
Xét tam giác ADC có:
\(\widehat{ACB}=\widehat{ADC}+\widehat{DAC}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{DAC}=\widehat{ACB}-\widehat{ACB}=60^0-30^0=30^0\)
\(\Rightarrow\widehat{DAC}=\widehat{ADC}=30^0\)
=> Tam giác ADC cân tại C
=> AC=DC=20m
Áp dụng tslg trong tam giác ABC vuông tại B:
\(AB=sinC.AC=sin60^0.20=10\sqrt{3}\left(m\right)\)
\(BC=cosC.AC=cos60^0.20=10\left(m\right)\)
C
30 tháng 3 2022
Những xóm làng trên cù lao sông Tiền có từ bao đời nay không hề biến động. Có những vườn cây mới trồng nhưng bạt ngàn là những vườn cây quả cổ thụ. Những rãnh nước được xẻ từ sông vào tưới tắm cho gốc cây bốn mùa ẩm ướt. Cóc, mận, mãng cầu, chôm chôm, vũ sữa, xoài tượng, xoài cát…
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 12 2020
Đề bài sai rồi em (hoặc là thiếu dữ liệu)
Không thể tính được khoảng cách giữa 2 hòn đảo chỉ với các số liệu này.
Giả sử người đó đứng ở vị trí A, hòn đảo thứ nhất ở vị trí B với \(\widehat{BAx}=40^0\) và \(AB=115\) nên điểm B cố định
Khi đó, nếu ta dựng tia Az sao cho \(\widehat{xAz}=60^0\) thì hòn đảo thứ 2 nằm ở 1 vị trí bất kì trên tia Az đều thỏa mãn bài toán
Nghĩa là khoảng cách giữa 2 hòn đảo thay đổi và không thể tính được. Em có thể đặt hòn đảo thứ 2 ở C hay D hay 1 điểm nào đó tùy thích. Rõ ràng là các đoạn BC và BD khác nhau về độ dài nhưng đều thỏa mãn yêu cầu bài toán.
