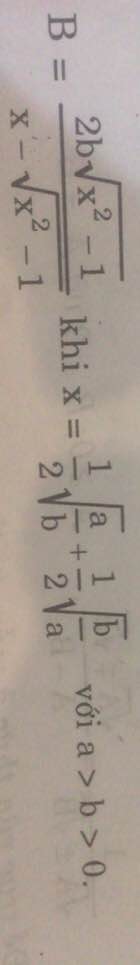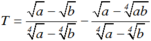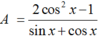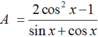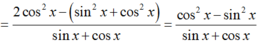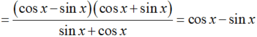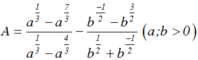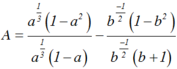Đơn giản biểu thức
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
9 tháng 9 2021
Lần sau đăng đề bạn nên gõ công thức cho gọn, đừng đăng ảnh dài oạch như thế này nhìn rất khó.
Lời giải:
Ta có:
\(x^2=\frac{1}{4}(\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}})^2=\frac{1}{4}(\frac{a}{b}+\frac{b}{a}+2)\)
\(\Rightarrow x^2-1=\frac{1}{4}(\frac{a}{b}+\frac{b}{a}-2)=\frac{1}{4}(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})^2\)
\(\Rightarrow \sqrt{x^2-1}=\frac{1}{2}|\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}|=\frac{1}{2}(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})\)
Do đó:
\(2b\sqrt{x^2-1}=b.\frac{a-b}{\sqrt{ab}}=(a-b).\sqrt{\frac{b}{a}}\)
\(x-\sqrt{x^2-1}=\frac{1}{2}[\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}-(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})]\)
\(=\sqrt{\frac{b}{a}}\)
$\Rightarrow B=a-b$
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2019
\(P=\frac{1-sin^2x.cos^2x}{cos^2x}-cos^2x=\frac{1}{cos^2x}-sin^2x-cos^2x\)
\(=1+tan^2x-\left(sin^2x+cos^2x\right)=1+tan^2x-1=tan^2x\)
\(M=\frac{2cos^2x-1}{sinx+cosx}=\frac{2cos^2x-\left(sin^2x+cos^2x\right)}{sinx+cosx}=\frac{cos^2x-sin^2x}{sinx+cosx}\)
\(\frac{\left(cosx-sinx\right)\left(cosx+sinx\right)}{sinx+cosx}=cosx-sinx\)
PT
ta được:
1
PT
1
PT
1
