Cho tam giác ABCD , gọi MN , PQ lần lượt là trung điểm AB ,BC , CD , DA và AC=BD . Chứng minh tứ giác MNPQ là hình thoi .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 8 2022
Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MNPQ là hình bình hành(5)
Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2=BD/2=MQ(3) và MN//AC
=>MN vuông góc với MQ(4)
Từ (3), (4)và (5) suy ra MNPQ là hình vuông
16 tháng 8 2022
a: Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MNPQ là hình bình hành(5)
Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2=BD/2=MQ(3) và MN//AC
=>MN vuông góc với MQ(4)
Từ (3), (4)và (5) suy ra MNPQ là hình vuông
16 tháng 8 2022
a: Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy a MQ//NP và MQ=NP
=>MNPQ là hình bình hành
b: Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2 và MN//AC
Để MNPQ là hình chữ nhật thì MN vuông góc với MQ
=>AC vuông góc với BD
CM
15 tháng 9 2017
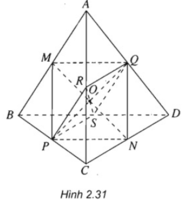
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
