Tìm nghiệm nguyên của phương trình 20y2 - 6xy = 150 - 15x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


PT
\(\Leftrightarrow20y^2-150=3x\left(2y-5\right)\)
\(\Leftrightarrow3x=\frac{20y^2-150}{2y-5}\)
De \(x\in Z\Rightarrow\frac{20y^2-150}{2y-5}\in Z\)
Dat \(M=\frac{20y^2-150}{2y-5}=5\left(2y+5\right)-\frac{25}{2y-5}\)
De \(3x=M=10y+25-\frac{25}{2y-5}\in Z\Rightarrow\frac{25}{2y-5}\in Z\Rightarrow2y-5\in\left\{-5;-1;1;5\right\}\)
Ta tim duoc
\(y_1=0;y_2=2;y_3=3;y_4=5\)
\(\Rightarrow x_1=x_3=30;x_2=70;x_4=70\)

\(20y^2-6xy=150-15x\)
\(\Leftrightarrow6xy-15x=20y^2-150\)
\(\Leftrightarrow3x\left(2y-5\right)=5\left(4y^2-25\right)-25\)
\(\Leftrightarrow5\left(4y^2-25\right)-3x\left(2y-5\right)=25\)
\(\Leftrightarrow5\left(2y-5\right)\left(2y+5\right)-3x\left(2y-5\right)=25\)
\(\Leftrightarrow\left(2y-5\right)\left[5\left(2y+5\right)-3x\right]=25\)
\(\Leftrightarrow\left(2y-5\right)\left(10y+25-3x\right)=25\)
Xét trường hợp:
\(\left(1\right)\left\{{}\begin{matrix}2y-5=1\\10y+25-3x=25\end{matrix}\right.\)
\(\left(2\right)\left\{{}\begin{matrix}2y-5=25\\10y+25-3x=1\end{matrix}\right.\)
\(\left(3\right)\left\{{}\begin{matrix}2y-5=-1\\10y+25-3x=-25\end{matrix}\right.\)
\(\left(4\right)\left\{{}\begin{matrix}2y-5=-25\\10y+25-3x=-1\end{matrix}\right.\)
\(\left(5\right)\left\{{}\begin{matrix}2y-5=5\\10y+25-3x=5\end{matrix}\right.\)
\(\left(6\right)\left\{{}\begin{matrix}2y-5=-5\\10y+25-3x=-5\end{matrix}\right.\)
P/s: Phiền bạn tự tính nghiệm rồi nhận hoặc loại nhé! Máy lỗi không hiển thị được. Srr...


cũng quy đồng, bạn đưa về pt :
6x -xy +6y +1 = 0
hay x( 6-y ) = -1-6y
x, y nguyên :
-1-6y chia hết cho 6-y
hay 6.(6-y) - 37 chia hết cho 6-y
vậy 6-y là ước của 37
bạn lại lập bảng ( hay giải từng cái cũng được ) tìm ra y , sau đó tìm x
( nhớ thử lại , và lấy x, y nguyên )

x2-6xy+5y2=121
<=> x2-xy-5xy+5y2=121
<=> x(x-y)-5y(x-y)=121
<=>(x-5y)(x-y)=121
Vì x,y nguyên nên x-5y và x-y có giá trị nguyên
=> x-5y và x-y là ước của 121
Mà Ư(21) ={ 1;-1;11;-11;121;-121}
TH1: x-5y=1 và x-y=121
=> x-5y-x+y=1-121
<=> -4y=-120
<=> y=30 ( là số nguyên)
=> x-30=121 <=> x=151 ( là số nguyên )
TH2: x-5y=-1 và x-y=-121
=> x-5y-x+y=120
<=>-4y=120
<=> y=-30( là số nguyên)
=> x+30=-121 <=>x=-151
TH3 : x-5y=121 và x-y=1
=> x-5y-x+y=121-1
<=> -4y=120 <=> y=-30( là số nguyên )
=> x= -29( là số nguyên )
TH4: x-5y=-121 và x-y=-1
=> x-5y-x+y= -121+1
<=> -4y=-120 <=> y=30( là số nguyên )
=> x-30=-1<=> x=29( là số nguyên)
TH5: x-5y=11 và x-y=11
=> x-5y-x+y=11-11
<=> -4y=0 <=> y=0( là số nguyên)
=> x=11( là số nguyên )
TH6 x-5y=-11 và x-y=-11
=> x-5y-x+y=-11+11
<=> -4y=0<=> y=0( là số nguyên)
=>x=-11 ( là số nguyên)
Ở trên đây mk không nhấn được thuộc Z nên mk viết là " là số nguyên" .Nếu bạn viết vào bài thì ghi dấu thuộc với Z nhé!!
Học tốt
pt <=> (x^2-xy)-(5xy-5y^2) = 121
<=> x.(x-y)-5y.(x-y) = 121
<=> (x-y).(x-5y) = 121
Đến đó bạn dùng ước bội mà giải nha
Tk mk


Đáp án B
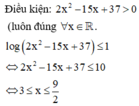
Vậy nghiệm nguyên dương của bất phương trình là x = {3;4}



\(20y^2-6xy=150-15x\)
\(\Leftrightarrow6xy-15x=20y^2-150\)
\(\Leftrightarrow3x\left(2y-5\right)=5\left(4y^2-25\right)-25\)
\(\Leftrightarrow3x\left(2y-5\right)=\left(2y-5\right)\left(10y+25\right)-25\)
\(\Leftrightarrow\left(2y-5\right)\left(10y+25-3x\right)=25\)
Đến đây thì dễ
P/s: Nguồn: Trên mạng :)
Cảm ơn bạn nha !!! 😊