Cho tam giác ABC có góc A = 40 độ, Góc AB = Góc AC. Gọi H là trung điểm của BC.
a) Tính góc ABC và góc ACB. Chứng minh AH vuông góc với BC
b) Đừng trung trực của AC cắt tia CB tại M. Tính góc MAh.
c) Trên tia đối của AM lấy N sao cho AN = BM. Chứng minh AM = CN
d) Vẽ CI vuông góc với MN tại I. Chứng minh I là trung điểm của MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 1 2022
a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
14 tháng 1 2022
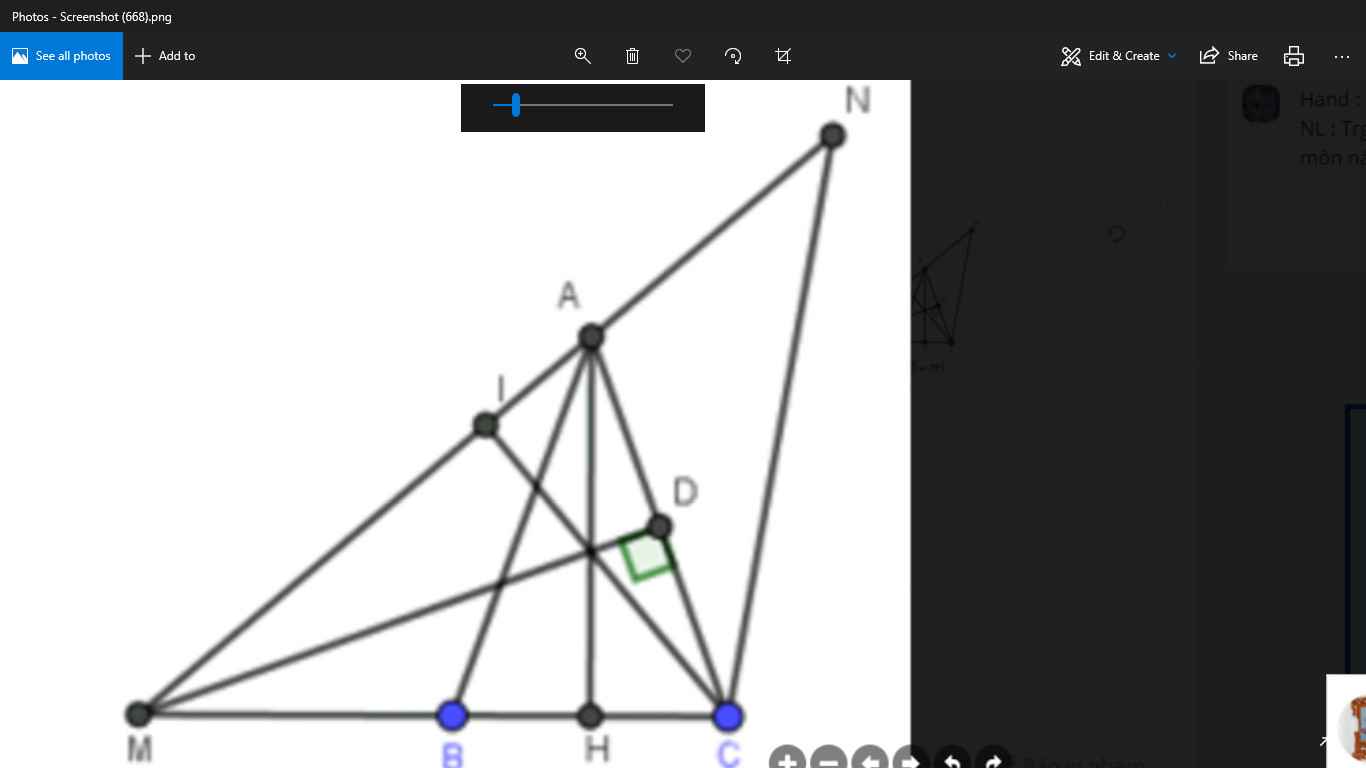
\(\text{a)}\Delta ABC\text{ cân tại }A\text{ có }\widehat{A}=40^0\)
\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
\(\text{Xét }\Delta ABH\text{ và }\Delta ACH\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
\(BH=CH\text{(H là trung điểm BC)}\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{ÂHB}=\widehat{AHC}\)
\(\text{mà }\widehat{AHB}+\widehat{AHC}=180^0\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^0\)
\(\Rightarrow AH\perp BC\)
\(\text{b)}\Delta AMC\text{ cân tại M}\text{ vì MD là đường trung trực}\)
\(\Rightarrow\widehat{MAD}=\widehat{MCD}=70^0\)
\(\text{Ta có:}\widehat{MAD}=\widehat{MAH}+\widehat{CAH}\)
\(\Rightarrow\widehat{MAH}=\widehat{MAD}-\widehat{CAH}=70^0-\dfrac{40^0}{2}=50^0\text{(vì AH là phân giác }\widehat{BAC}\text{)}\)
\(\text{c)Xét }\Delta ABM\text{ và }\Delta CAN\text{ có:}\)
\(BM=AN\text{(cách lấy điểm N)}\)
\(AB=AC\left(cmt\right)\)
\(\widehat{ABM}=\widehat{CAN}=180^0-70^0=110^0\)
\(\Rightarrow\Delta ABM=\Delta CAN\left(c.g.c\right)\)
\(\Rightarrow AM=AN\text{(hai cạnh tương ứng)}\)
\(\text{d)Xét }\Delta MIC\text{ và }\Delta NIC\text{ có:}\)
\(IC\text{ cạnh chung}\)
\(\widehat{MIC}=\widehat{NIC}=90^0\)
\(\widehat{IMC}=\widehat{INC}\text{(vì }\Delta ABM=\Delta CAN\text{)}\)
\(\Rightarrow\Delta MIC=\Delta NIC\left(gn.cgv\right)\)
\(\Rightarrow MI=NI\)
\(\Rightarrow\text{I là trung điểm MN}\)
DG
23 tháng 5 2020
jfccfffcfffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
18 tháng 2 2022
a: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
b: Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
c: Ta có: M nằm trên đường trung trực của AC
nên MA=MC
hay ΔMAC cân tại M
17 tháng 12 2022
a: ΔABC cân tại A
nên góc ABC=góc ACB
ΔBCA cân tại A
mà AH la trung tuyến
nên AH vuônggóc với BC
b: Xét ΔDMH vuông tại M và ΔDMC vuông tại M có
DM chung
MH=MC
Do đó: ΔDMH=ΔDMC
c: Xét ΔAHC có MD//AC
nên AD/DC=HM/MC=1
=>D là trung điểm của CA
Xét ΔCBA có CD/CA=CH/CB
nên HD//AB
