cho hai đường thẳng d: y=x+2m, d'= 3x+2 (m là tham số)
chứng minh hai đường thẳng d,d' cắt nhau và tìm tọa độ giao điểm của chúng
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 5 2019
Đáp án B
+ Tọa độ giao điểm của hai đường thẳng d và d’ là nghiệm của hệ phương trình:
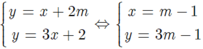
suy ra d và d’ cắt nhau tại M( m-1; 3m-1)
+ Vì ba đường thẳng d; d’ ; d’’ đồng quy nên d’’ qua M ta có
3m-1= -m( m-1) + 2 hay m2+ 2m-3=0
Suy ra m=1 hoặc m= -3
Với m= 1 ta có ba đường thẳng là d: y= x+ 2; d’ : y= 3x+ 2 và d’’: y= -x+ 2 phân biệt và đồng quy tại M(0; 2).
Với m= -3 ta có d và d’’ trùng nhau suy ra m= -3 không thỏa mãn
Vậy m= 1 là giá trị cần tìm.
Chọn B.
CM
28 tháng 9 2019
Ta thấy d: y = ( m + 2 ) x – m c ó a = m + 2 v à d ’ : y = − 2 x − 2 m + 1 c ó a ’ = − 2
+) Điều kiện để y = ( m + 2 ) x – m là hàm số bậc nhất m + 2 ≠ 0 ⇔ m ≠ − 2
+) Để d ≡ d ’ ⇔ a = a ' b = b ' ⇔ m + 2 = − 2 − m = − 2 m + 1 ⇔ m = − 4 m = 1 (vô lý)
Vậy không có giá trị nào của m để d ≡ d ’
Đáp án cần chọn là: D
CM
12 tháng 3 2018
Ta thấy d: y = ( 2 m − 3 ) x – 2 c ó a = 2 m – 3 ; b = − 2 v à d ’ : y = − x + m + 1 c ó a ’ = − 1 ; b ’ = m + 1
Điều kiện để y = ( 2 m − 3 ) x – 2 là hàm số bậc nhất là: a ≠ 0 ⇔ 2 m – 3 ≠ 0 ⇔ m ≠ 3 2
Để d // d’ thì a = a ' b ≠ b ' ⇔ 2 m − 3 = − 1 − 2 ≠ m + 1 ⇔ m = 1 m ≠ − 3 ⇔ m = 1 (TM)
Đáp án cần chọn là: A
Phương trình hoành độ giao điểm là:
x+2m=3x+2
=>-2x=-2m+2
=>x=m-1
Khi x=m-1 thì y=m-1+2m=3m-1