cho đường tròn tâm O đường kính AB cố định. Ax và Ay là hai tia thay đổi luôn tạo với nhau góc 60độ và lần lượt cắt đường tròn (O) tại M và N. Đường thẳng BN cắt Ax tại E, đường thẳng BM cắt Ay tại F. Gọi K là trung điểm của đoạn thẳng EF.
a. Chứng minh rằng đoạn thẳng EF có độ dài không đổi
b. Chứng minh rằng OMKN là tứ giác nội tiếp
c. Khi AMN là tam giác đều, gọi C là điểm trên đường tròn (O) khác A, khác N. Đường thẳng qua M và vuông góc với AC cắt NC tại D. Xác định vị trí của điểm C để diện tích am giác MCD là lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét ΔBHA có
BD vừa là đường cao, vừa là phân giác
=>ΔBHA cân tại B
=>D là trung điểm của AH
góc EAD=1/2*sđ cung AD
góc FAD=góc FBC=1/2*sđ cung DC
mà sđ cung AD=sđ cung DC
nên góc EAD=góc FAD
=>AD là phân giác của góc EAF
=>D là trung điểm của EF
Xét tứ giác AEHF có
D là trung điểm chung của AH và EF
AH vuông góc EF
=>AEHF là hình thoi
a: góc ADB=1/2*180=90 độ
=>BD vuông góc AH
góc ACB=1/2*180=90 độ
=>AC vuông góc HB
góc HDF+góc HCF=180 độ
=>HDFC nội tiếp

a: góc OMA=1/2*sđ cung OA=90 độ
góc ONA=1/2*sđ cung OA=90 độ
Vì góc OMA=góc ONA=góc MAN=90 độ
nên AMON là hình chữ nhật
b: ΔOAB cân tại O
mà OM là đường cao
nên Mlà trung điểm của AB
ΔOAC cân tại O
mà ON là đường cao
nên N là trung điểm của AC
Xet ΔACB có AM/AB=AN/AC
nên MN//BC

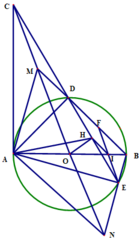
a) Ta có
C A B ⏜ = 90 0 O H C ⏜ = 90 0 ⇒ C A B ⏜ + O H C ⏜ = 180 0
Vậy tứ giác AOHC nội tiếp.
b) Ta có C A D ⏜ = A E C ⏜ , A C E ⏜ chung suy ra Δ A C D ~ Δ E C A (g.g)
⇒ C A C E = A D A E ⇒ A C . A E = A D . C E
c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F ⇒ H E I ⏜ = H C O ⏜ .
Vì tứ giác AOHC nội tiếp ⇒ H A O ⏜ = H C O ⏜ = H E I ⏜ .
Suy ra tứ giác AHIE nội tiếp ⇒ I H E ⏜ = I A E ⏜ = B D E ⏜ ⇒ H I / / B D .
Mà H là trung điểm của DE=> I là trung điểm của EF. Có EF//MN và IE= IF
=> O là trung điểm của đoạn thẳng MN.
Suy ra tứ giác AMBN là hình bình hành => AM//BN.
Ai làm hộ mình với