Cho tam giác nhọn ABC và điểm M trong tam giác đó.Xác định vị trí của điểm M sao cho MA.BC+MB.AC+MC.AB đạt giá trị nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



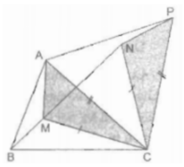
Trong ∆ ABC ta lấy điểm M. Nối MA, MB, MC.
Ta cần làm xuất hiện tổng MA + MB + MC sau đó tìm điều kiện để tổng đó nhỏ nhất.
Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN.
Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC. Khi đó, CA = CP
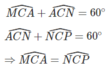
Xét ∆ AMC và ∆ PNC:
CM = CN (vì ΔMCN đều)
CA = CP (vì ΔAPC đều)
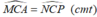
Suy ra: ∆ AMC = ∆ PNC (c.g.c)
⇒ PN = AM
MA + MB + MC = NP + MB + MN
Ta có ∆ ABC cho trước nên điểm P cố định nên BM + MN + NP ngắn nhất khi 4 điểm B, M, N, P thẳng hàng.


a,
Kẻ BE,CF vuông góc với AM.
Ta có:
MA.BC = MA.(BP+CP) ≥ MA.(BE+CF) = 2 SABM + 2 SCAM
Tuong tu:
MB.CA ≥ 2SBCM + 2 SABM
MC.AB ≥ 2SCAM + 2 SBCM
Suy ra:
MA.BC + MB.CA + MC.AB ≥ 2 ( 2 SABM + 2SBCM + 2SCAM) = 4SABC
dpcm.
Dấu = xảy ra khi M là trực tâm.