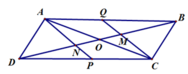
Cho hình bình hành ABCD, trên đường chéo BD lấy hai điểm M, N sao cho BM = MN = ND. Gọi I là giao điểm của AN và DC, K là giao điểm của CM và AB, O là giao điểm của AC và BD. Chứng minh rằng ba điểm I, O, K thẳng hàng.
mn giúp em sớm đc ko ạ, em đang cần gấp mà nghĩ ko ra, em cảm ơn


a) Xét ∆AND và ∆CMB có:
BM=DN (giả thiết)
AD=BC(các cạnh đối bằng nhau)
góc ADN=góc CBM( so le trong)
Vậy ∆AND=∆CMB( cạnh góc cạnh)
=> AN=CM( 2 cạnh tương ứng)( điều phải chứng minh)
b)AN//CM( góc ANM= góc CMN so le trong)và AN=CM( chứng minh trên)
=> Tứ giác AMCN là hình bình hành(điều phải chứng minh)
c)AN//CM mà N thuộc AI và M thuộc CK
->AI//CK
AB//DC mà K thuộc AB và I thuộc DC
->AK//DI
Vậy tứ giác AKCI là hình bình hành( các cạnh đối song song)
=> AC và KI là đường chéo của hình bình hành AKCI
=> AO= OC; KO=OI ( hai đường chéo cắt nhau tại trung điểm mỗi đường)
Vậy K,O,I cùng nằm trên cùng 1 đường thẳng( điều phải chứng minh)
hok tốt