Mọi người ơi giúp đỡ em với ạ. 

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


11)\(\dfrac{3x+1}{x-5}+\dfrac{2x}{x-5}=\dfrac{3x+2x+1}{x-5}=\dfrac{5x+1}{x-5}\)
12)\(\dfrac{4-x^2}{x-3}+\dfrac{2}{x^2-9}=\dfrac{4-x^2}{x-3}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{\left(4-x^2\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{2+\left(2-x\right)\left(2+x\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
13)
\(\dfrac{3}{4x-2}+\dfrac{2x}{4x^2-1}=\dfrac{3}{2\left(2x-1\right)}+\dfrac{2x}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{3\left(2x+1\right)}{2\left(2x-1\right)\left(2x+1\right)}+\dfrac{2.2x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{6x+3+4x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{10x+3}{2\left(2x-1\right)\left(2x+1\right)}\)
14)
\(\dfrac{2x+1}{2x-4}+\dfrac{5}{x^2-4}=\dfrac{2x+1}{2\left(x-2\right)}+\dfrac{5}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(2x+1\right)\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\dfrac{5.2}{2\left(x-2\right)\left(x+2\right)}=\dfrac{2x^2+5x+12}{2\left(x-2\right)\left(x+2\right)}\)

Đề 1:
Bài 1:
\(a,=\sqrt{\left(\sqrt{7}+1\right)^2}-\left|-1+\sqrt{7}\right|=\sqrt{7}+1-\sqrt{7}+1=2\\ b,=2\sqrt{2}-4\sqrt{2}-5\sqrt{2}+\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}-7\sqrt{2}=\dfrac{-13\sqrt{2}}{\sqrt{2}}\)
Bài 2:
\(PT\Leftrightarrow\sqrt{\left(x-\dfrac{1}{2}\right)^2}=\dfrac{1}{2}\Leftrightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}+\dfrac{1}{2}=1\\x=-\dfrac{1}{2}+\dfrac{1}{2}=0\end{matrix}\right.\)
Bài 3:
\(a,M=\dfrac{a-2\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{2\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)^2\left(\sqrt{a}+1\right)}=\dfrac{2}{\sqrt{a}+1}\\ b,M< 1\Leftrightarrow\dfrac{2}{\sqrt{a}+1}-1< 0\Leftrightarrow\dfrac{1-\sqrt{a}}{\sqrt{a}+1}< 0\\ \Leftrightarrow1-\sqrt{a}< 0\left(\sqrt{a}+1>0\right)\\ \Leftrightarrow a>1\)

Câu 1:
\(\left(4x+3\right)\left(3x^2+x-2\right)\left(2x^2-3x-5\right)=0\\ \Leftrightarrow\left(4x+3\right)\left(3x-2\right)\left(x+1\right)\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=-1\\x=\dfrac{2}{3}\\x=\dfrac{5}{2}\end{matrix}\right.\\ \Leftrightarrow A=\left\{-1;-\dfrac{3}{4};\dfrac{2}{3};\dfrac{5}{2}\right\}\)
Câu 2:
\(\left(x^2-4\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=3\end{matrix}\right.\Leftrightarrow A=\left\{-2;2;3\right\}\\ \left|5x\right|-11\le0\Leftrightarrow\left|5x\right|\le11\Leftrightarrow-11\le5x\le11\\ \Leftrightarrow-\dfrac{11}{5}\le x\le\dfrac{11}{5}\\ \Leftrightarrow B=\left[-\dfrac{11}{5};\dfrac{11}{5}\right]\)
\(\Leftrightarrow A\cap B=\left\{-2;2\right\}\\ A\cup B=\left[-\dfrac{11}{5};3\right]\\ A\B=\left\{3\right\}\)
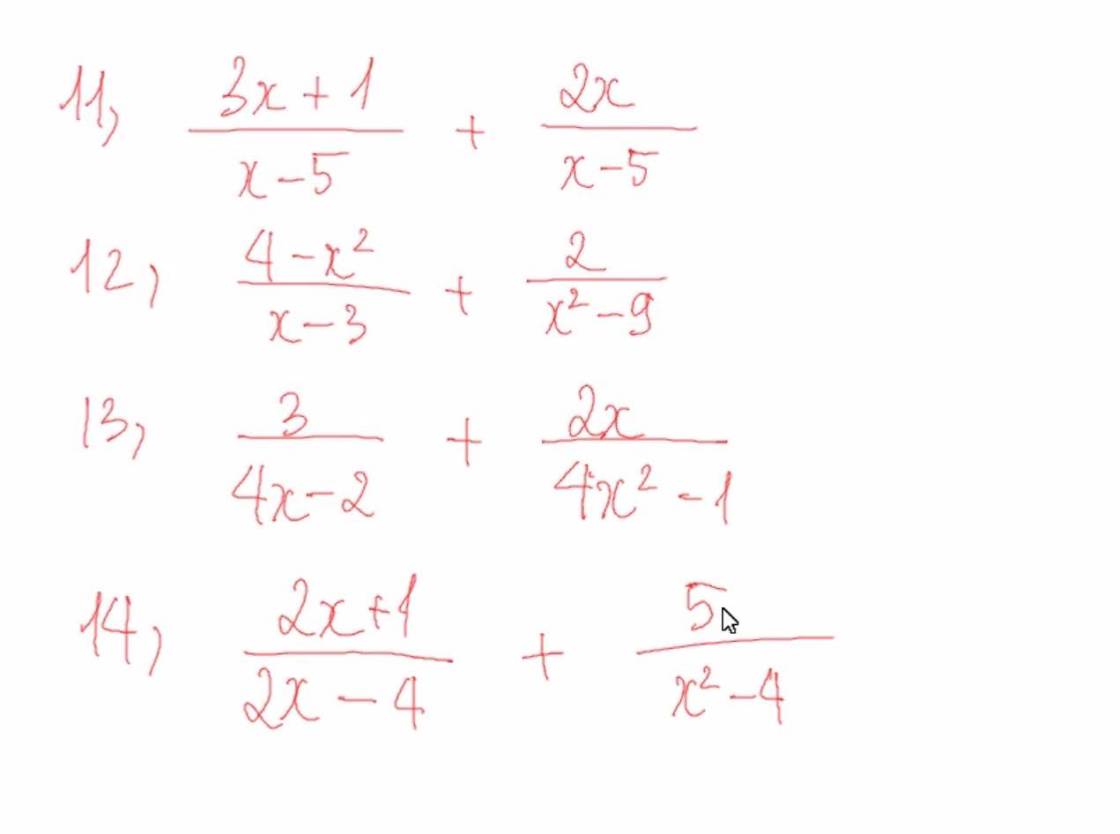
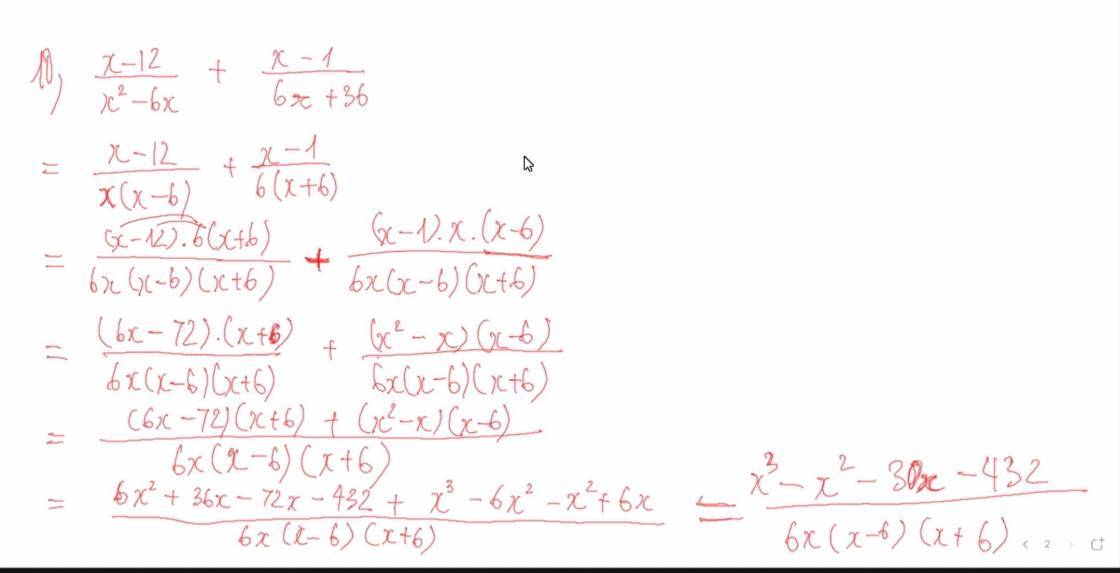


 giúp mình với mọi người ơi, tuy hơi dài nhưng mong các anh, chị giúp đỡ ạ, đây là bt part 1 còn bt part 2 nữa ạ! Mong anh chị giúp em làm nhanh nhất có thể ạ
giúp mình với mọi người ơi, tuy hơi dài nhưng mong các anh, chị giúp đỡ ạ, đây là bt part 1 còn bt part 2 nữa ạ! Mong anh chị giúp em làm nhanh nhất có thể ạ

 b2:
b2: b3:
b3: b4:
b4:

