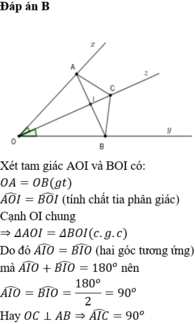
Cho góc XOY, gọi OZ là tia phân giác góc XOY. Trên OX lấy điểm A, trên OY lấy điểm B sao cho OA = OB. Lấy điểm I trên OZ sao cho OI>OA. So sánh IA và IB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 9 2021
a: Xét ΔAOI và ΔBOI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔAOI=ΔBOI
Suy ra: IA=IB
9 tháng 12 2021
a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
13 tháng 12 2021
a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
13 tháng 12 2021
\(a,\left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OI\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOI=\Delta BOI\left(c.g.c\right)\\ b,\text{Gọi }AB\cap OI=\left\{H\right\}\\ \left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OH\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOH=\Delta BOH\left(c.g.c\right)\\ \Rightarrow\widehat{AHO}=\widehat{BHO}\\ \text{Mà }\widehat{AHO}+\widehat{BHO}=180^0\\ \Rightarrow\widehat{AHO}=\widehat{BHO}=90^0\\ \Rightarrow OI\bot AB\)
OE
21 tháng 12 2021
a: Xét tứ giác BOAE có
I là trung điểm của BA
I là trung điểm của OE
Do đó: BOAE là hình bình hành
Suy ra: BE//OA
27 tháng 11 2021
a
xét tam giác AOD và BCD có:
góc D chung,OB=OA,OC=OD
=>tam giác AOD=BCD=>BC=AD
vì OC+CA=OA,OD+DB=OB mà OC=OD,OA=OB
=>AC=BD
xét tam giác ADB và BCA có:
AC=BD,AB chung,BC=AD
=>ADB=BCA
b
xét tam giác OIA và OIB có
OA=OB,OI chung,IA=IB
=>tam giác OIA=OIB=>góc AOI=góc BOI=>OI là phân giác góc xOy
