Cạnh huyền của một tam giác vuông cân bằng 49cm. Tính mỗi cạnh góc vuông của tam giác đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
8 tháng 5 2022
Lời giải:
Gọi độ dài cạnh góc vuông lần lượt là $a$ và $b$ ($a>b>0$) (cm)
Áp dụng định lý Pitago: $a^2+b^2=60^2=3600(*)$
$a-b=12$
$\Leftrightarrow a=b+12$. Thay vào $(*)$ thì:
$(b+12)^2+b^2=3600$
$\Leftrightarrow 2b^2+24b-3456=0$
$\Leftrightarrow b^2+12b-1728=0$
$\Leftrightarrow (b-36)(b+48)=0$
Do $b>0$ nên $b=36$ (cm)
$a=b+12=36+12=48$ (cm)
HP
8 tháng 5 2022
Gọi x là cạnh góc vuông dài (cm) (x > 0)
Độ dài cạnh góc vuông ngắn là: x - 12 (cm)
Theo định lý Pi - ta - go, ta có phương trình:
\(x^2+\left(x-12\right)^2=60^2\)
\(\Leftrightarrow x^2+x^2+24x+144=3600\)
\(\Leftrightarrow2x^2+24x-3456=0\)
\(\Delta'=12^2-\left(-3456\right).2=7056>0\)
Do \(\Delta'>0\) nên phương trình có 2 nghiệm phân biệt:
\(x_1=\dfrac{-12+\sqrt{7056}}{2}=36\left(tm\right)\)
\(x_2=\dfrac{-12-\sqrt{7056}}{2}=-48\left(ktm\right)\)
Vậy độ dài cạnh góc vuông dài là 36 cm
Độ dài canh góc vuông ngắn là: 36 - 12 = 24 (cm)
CM
17 tháng 3 2017
Xét tam giác ABC vuông tại A với AB > AC, gọi AH là đường cao kẻ từ A thì ta có:
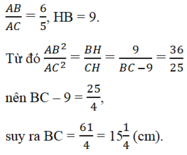
Gọi độ dài cạnh góc vuông của tam giác đó là a
Theo định lí Pitago :
a2 + a2 = 492
=> 2a2 = 2401
=> a2 = 2401 : 2 = 1200.5
=> a = \(\frac{49\sqrt{2}}{2}\)
ta có: tam giác ABC vuông cân tại A
=> AB = AC ( định lí) => AB2 = AC2
Xét tam giác ABC vuông tại A
=> AB2 + AC2 = 492 ( py-ta-go)
AB2 + AB2 = 492
2.AB2 = 492
AB2 = 1200,5
\(\Rightarrow AB=\sqrt{1200,5}cm\)
=> \(AB=AC=\sqrt{1200,5}cm\)