Chứng tỏ rằng 2110 -1 chia hết cho 200
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 7 2019
* Áp dụng hằng đẳng thức:
Ta có:
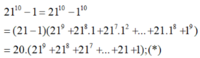
Ta có:
gồm có 10 số hạng
có chữ số tận cùng bằng 0. Do đó, ta có thể viết:
Thay vào (*) ta được:
2110 - 1 = 20.10.A = 200A
Suy ra: 2110 - 1 chia hết cho 200.
7 tháng 9 2019
link tham khảo
ccaau hỏi của ng duy mạnh
link : https://olm.vn/hoi-dap/detail/60197622644.html
hok tót
DH
3 tháng 9 2019
Ta có: 2110 - 1 = (21 - 1)(219 + 218 + 217 + ... + 21 + 1)
= 20.10M (M ∈ N)
= 200.M chia hết cho 200.
KS
1
NM
Nguyễn Minh Quang
Giáo viên
2 tháng 5 2021
a. ta có \(11\equiv1mod10\Rightarrow11^{200}\equiv1mod10\)
nên \(11^{200}-1\equiv0mod10\). Vậy \(11^{200}-1\) chia hết cho 10.
b. ta có \(12\equiv2mod10\Rightarrow12^{200}\equiv2^{200}mod10\)
nên \(12^{200}-2^{200}\equiv0mod10\). Vậy \(12^{200}-2^{200}\) chia hết cho 10.
KT
0
KS
1
24 tháng 7 2016
Ta có:
162008 - 8200
= (...6) - (84)50
= (...6) - (...6)50
= (...6) - (...6)
= (...0) chia hết cho 10
24 tháng 7 2016
Ta có:
162008 - 8200
= (...6) - (84)50
= (...6) - (...6)50
= (...6) - (...6)
= (...0) chia hết cho 10
DN
1
30 tháng 10 2015
a) A=5(1+5)+53(1+5)+...+5199(1+5)
=(1+5)(5+53+....+5199) chia hết cho 6
b) A:31 dư 30 hay A-30 chia hết cho 31
Ta có A=5(1+5+52)+54(1+5+52)+57(1+5+52)+.....+598(1+5+52)
31(5+54+57+...+599) chia hết cho 31. Nên A chia cho 31 không dư
21 tháng 10 2021
\(21^2\equiv1\left(mod8\right)\Leftrightarrow21^{10}\equiv1^5=1\left(mod8\right)\\ \Leftrightarrow21^{10}-1\equiv0\left(mod8\right)\\ \Leftrightarrow21^{10}-1⋮8\left(1\right)\\ 21^5\equiv1\left(mod25\right)\Leftrightarrow21^{10}\equiv1^2=1\left(mod25\right)\\ \Leftrightarrow21^{10}-1\equiv0\left(mod25\right)\\ \Leftrightarrow21^{10}-1⋮25\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow21^{10}-1⋮25\cdot8=200\)
nếu bạn là hs chuyên toán thì mình giải theo cách này
ta thấy 200=8.25 (phân tích thừa số nguyên tố)
ta cần chứng minh 2110-1 đông dư 0 (mod8) ta co 212 đồng dư 1 (mod 8) <=> 2110-1 đồng dư o mod 8 (1)
2110-1 dong du 0 (mod 25) ta có 215 đồng dư 1 (mod 25) <=> 2110-1 đồng dư 0 mod 25 (2)
từ (1) và (2)
tao suy ra..............