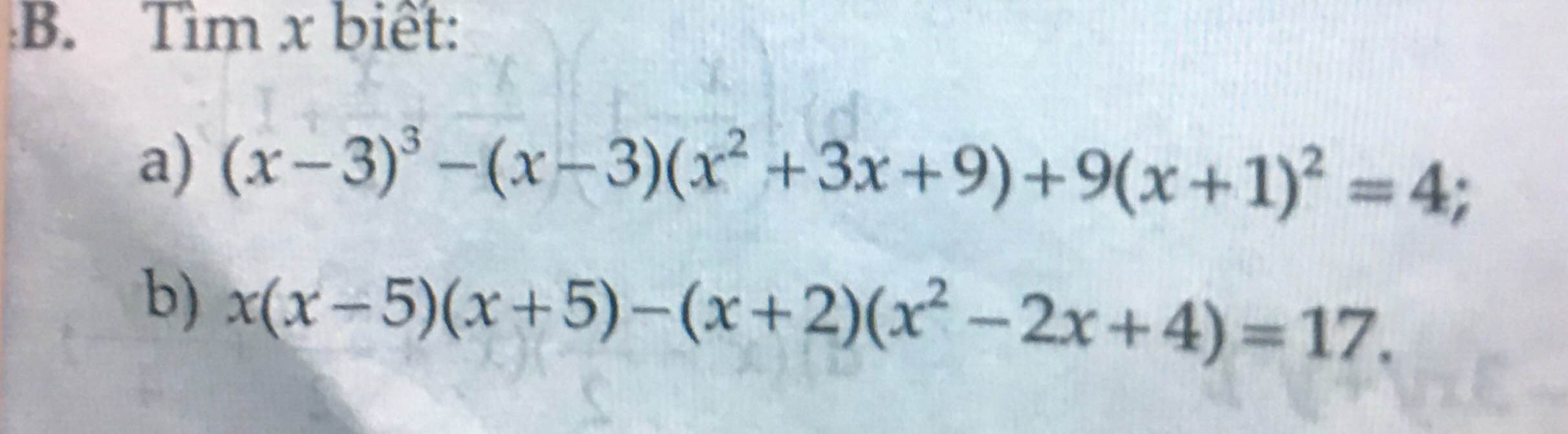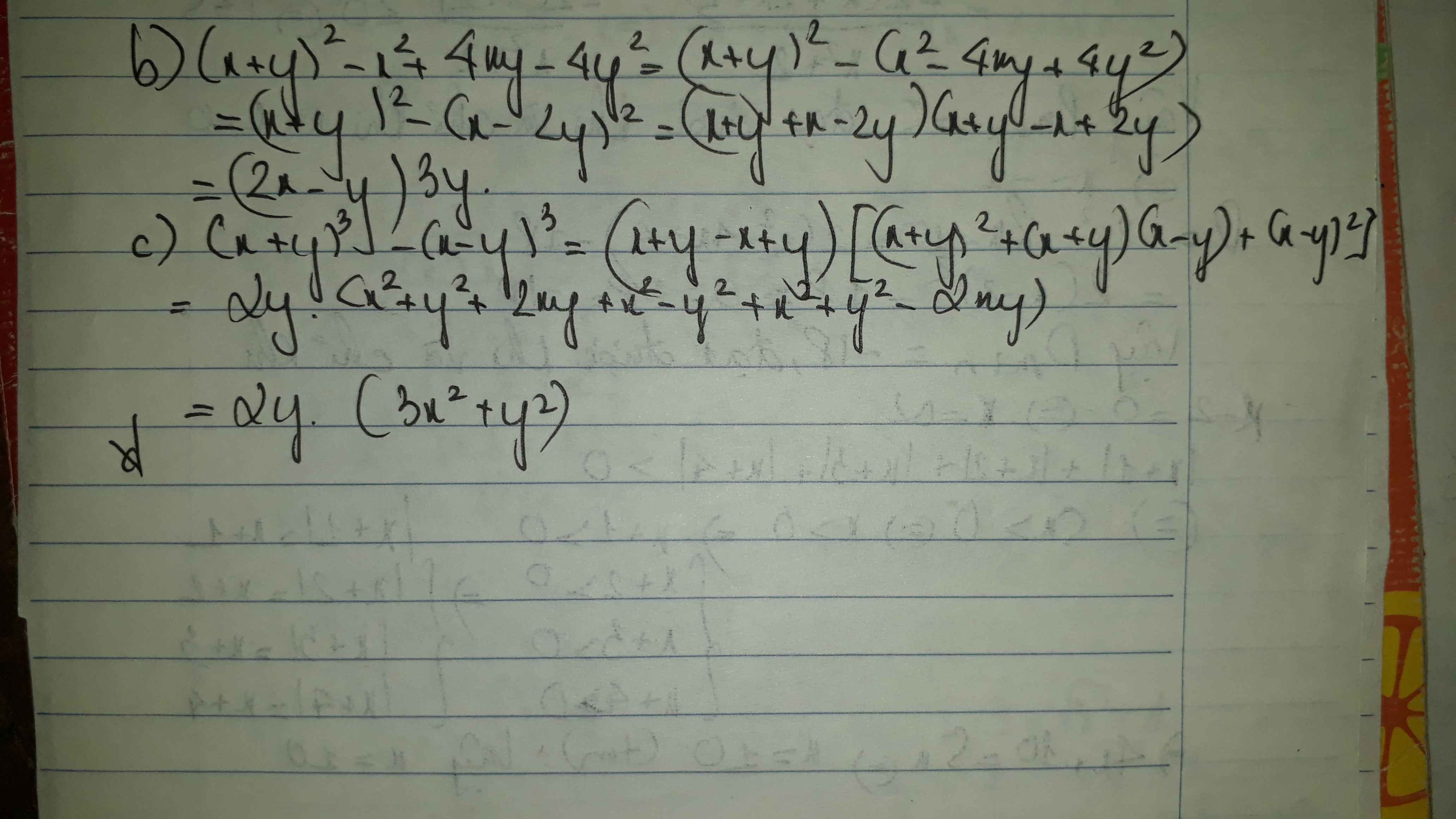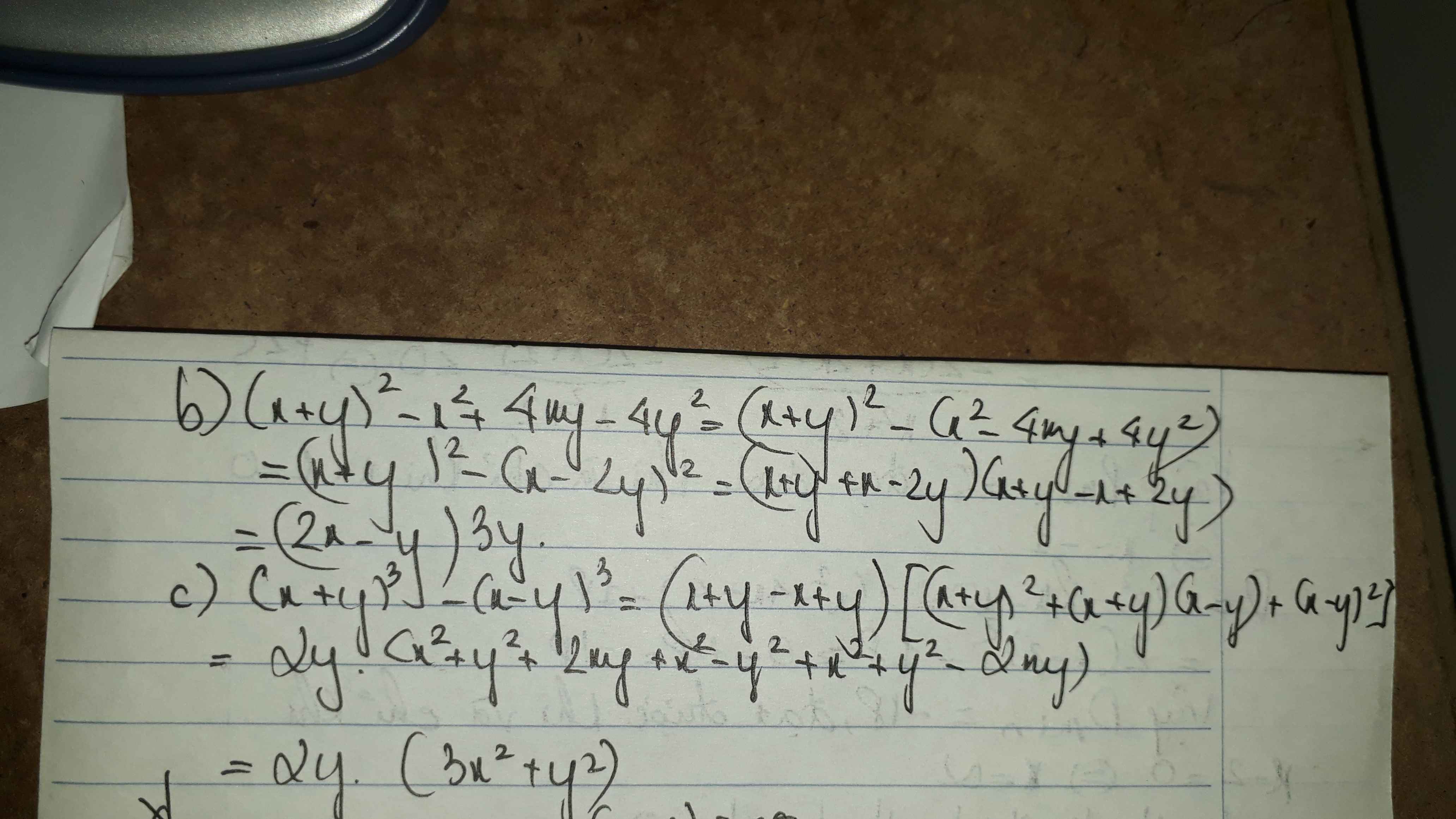Giúp mik gấp với mọi người ơi 😭😭😭
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1.
Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
\(;a_i\ne a_j\)
Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.
5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)
\(\Rightarrow\)Có \(A_8^5\) cách.
Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.

a: Ta có: \(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+9\left(x+1\right)^2=4\)
\(\Leftrightarrow x^3-9x^2+27x-27-x^3+27+9x^2+18x+9=4\)
\(\Leftrightarrow45x=-5\)
hay \(x=-\dfrac{1}{9}\)
b: Ta có: \(x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)=17\)
\(\Leftrightarrow x^3-25x-x^3-8=17\)
\(\Leftrightarrow-25x=25\)
hay x=-1


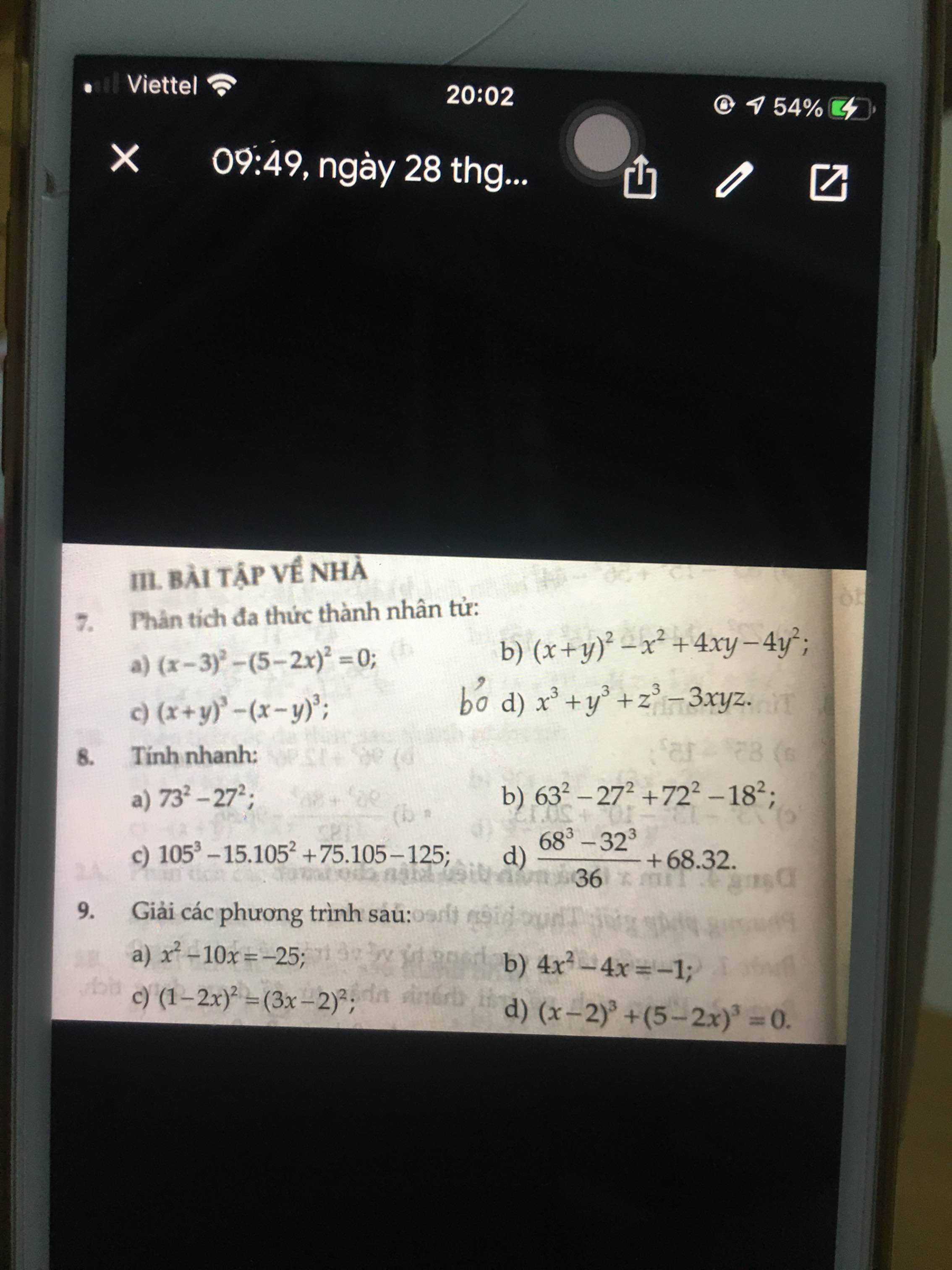
Bài 9:
a: Ta có: \(x^2-10x=-25\)
\(\Leftrightarrow x^2-10x+25=0\)
\(\Leftrightarrow x-5=0\)
hay x=5
b: ta có: \(4x^2-4x=-1\)
\(\Leftrightarrow4x^2-4x+1=0\)
\(\Leftrightarrow2x-1=0\)
hay \(x=\dfrac{1}{2}\)
c: Ta có: \(\left(2x-1\right)^2=\left(3x-2\right)^2\)
\(\Leftrightarrow\left(3x-2\right)^2-\left(2x-1\right)^2=0\)
\(\Leftrightarrow\left(3x-2-2x+1\right)\left(3x-2+2x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(5x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{5}\end{matrix}\right.\)

Bài 8:
a: \(73^2-27^2=\left(73-27\right)\left(73+27\right)=4600\)
b: \(63^2-27^2+72^2-18^2\)
\(=\left(63-18\right)\left(63+18\right)+\left(72-27\right)\left(72+27\right)\)
\(=45\cdot\left(63+18+72+27\right)\)
\(=45\cdot180=8100\)

b: Ta có: \(\left(x+y\right)^2-x^2+4xy-4y^2\)
\(=\left(x+y\right)^2-\left(x-2y\right)^2\)
\(=\left(x+y-x+2y\right)\left(x+y+x-2y\right)\)
\(=3y\cdot\left(2x-y\right)\)
c: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=2y^3+6x^2y\)
\(=2y\left(3x^2+y^2\right)\)