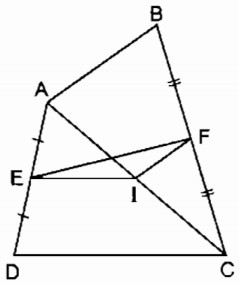
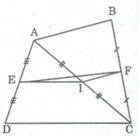
Bài 1: Cho tứ giác ABCD. Gọi E, F, I là trung điểm của AD, BC, AC. Chứng minh rằng:
a) EI // CD; IF // AB.
b) EF ≤ (AB+CD)/2
Bài 4: Cho tam giác ABC có đường truyến BD và CE cắt nhau tại G. Gọi I, K là trung điểm GB, GC. Chứng minh DE// IK và DE = IK.
Bài 5: Cho tam giác ABC có đường trung tuyến BD và CE. Gọi M, N là trung điểm BE, CD. Gọi MN cắt BD tại I và MN cắt CE tại I. Chứng minh MI = IK = KN