Mn giải giúp em với ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3N
1
YN
2 tháng 3 2022
1 The distance from my home to school is about 3 km
2 My mum used to live in a small village when she was small
3 Despite being a millionaire , he lives in a small flat
4 when does the festive take place ?
5 It is about two kilometres from my home to school
6 he didn't use to ride his bike to school
7 Despite having a test tomrrow , they are still watching TV now
TM
0
LT
0
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2021
33.
\(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x=cosx\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)=cosx\)
So sánh nó với \(cos\left(2x-a\right)=cosx\)
\(\Rightarrow a=\dfrac{\pi}{3}\)
34.
ĐKXĐ:
\(sinx-cosx\ne0\)
\(\Leftrightarrow tanx\ne1\)
\(\Leftrightarrow x\ne\dfrac{\pi}{4}+k\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2021
35.
\(y=2\left(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx\right)-2=2sin\left(x-\dfrac{\pi}{6}\right)-2\)
Do \(-1\le sin\left(x-\dfrac{\pi}{6}\right)\le1\Rightarrow-4\le y\le0\)
Tập giá trị: \(\left[-4;0\right]\)
36.
\(y=cos2x\) tuần hoàn chu kì \(\dfrac{2\pi}{\left|2\right|}=\pi\)
\(y=sinx\) tuàn hoàn chu kì \(\dfrac{2\pi}{\left|1\right|}=2\pi\)
\(y=tan2x\) tuần hoàn chu kì \(\dfrac{\pi}{\left|2\right|}=\dfrac{\pi}{2}\)
\(y=cot4x\) tuần hoàn chu kì \(\dfrac{\pi}{\left|4\right|}=\dfrac{\pi}{4}\)
LD
2
22 tháng 10 2021
\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
22 tháng 10 2021
a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)
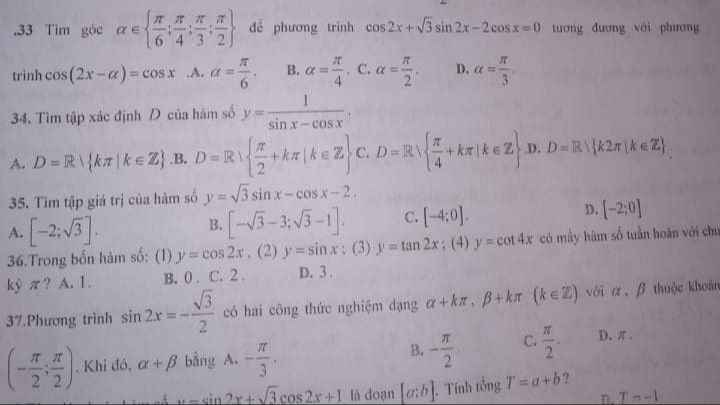
Mn giải giúp em với ạ