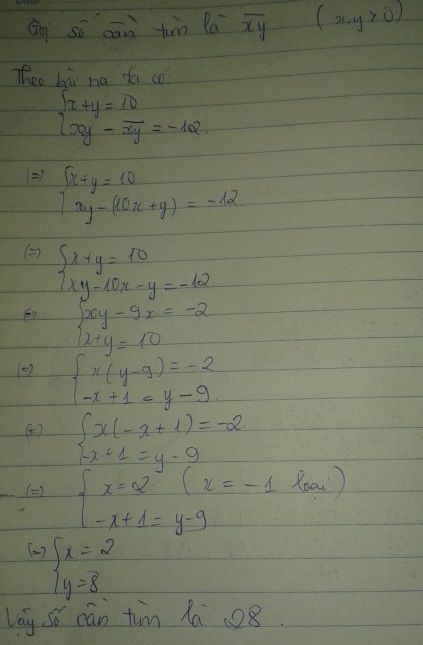Cho 2 chữ số 2;4;6;8 .Hỏi có thể lập bao nhiêu số thập phân có 4 chữ số từ các số đã cho ( Mỗi chữ số chỉ xuất hiện một lần trong mỗi số thập phân )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 1 2017
- số có 2 chữ số được viết dưới dạng 10+a ( với a là số nguyên dương).
- khi thêm chữ số 3 vào bên trái,ta có số có 3 chữ số sau: 300+10+a
- Khi đó số có 3 chữ số gấp 5 lần chữ số ban đầu, ta có: 300+10+a = 5(10+a)
310+a=50+5a
4a=260
a=65.
Vậy số đã cho là 10+65=75
DD
Đoàn Đức Hà
Giáo viên
6 tháng 6 2021
Gọi số có hai chữ số là \(\overline{ab}\).
Số khi viết ngược lại sẽ là: \(\overline{ba}\).
Tổng hai số là:
\(\overline{ab}+\overline{ba}=10\times a+b+10\times b+a=11\times\left(a+b\right)\)
do đó tổng hai số chia hết cho \(11\).
8 tháng 6 2021
Một ô tô khởi hành tại lúc 4 giờ sáng để đi đến b với vận tốc 60 km / h . Đến sau đó 1 giờ , một ô tô khác đi từ B về A với vận tốc 70 km /h . Hai xe gặp nhau lúc 8h . Hỏi
a, Khoảng cách từ A đến B
b, Xe đi từ A , đến B lúc mấy giờ
c, Xe đi từ B đến A lúc mấy giờ
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
15 tháng 6 2021
Đặt số lớn là \(\overline{ab}\) và số nhỏ là \(\overline{cd}\)
Theo đề bài
\(\overline{abcd}-\overline{cdab}=693\)
\(\Rightarrow100x\overline{ab}+\overline{cd}-100x\overline{cd}-\overline{ab}=693\)
\(\Rightarrow99x\overline{ab}-99x\overline{cd}=693\Rightarrow\overline{ab}-\overline{cd}=7\)
Số lớn \(\overline{ab}\) là
(41+7):2=24
Số bé \(\overline{cd}\) là
41-24=17
BT
16 tháng 12 2017
Gọi số đó là ab (0 < a\(\le\)9;0\(\le\)b\(\le\)9)
Khi viết thêm 2 vào giữa sẽ có dạng a2b
Theo bài ra: a2b-ab=110
<=> 100a+20+b-10a-b=110
<=> 90a=90 => a=1
=> a2b giờ sẽ là 12b
Số đó chia hết cho 3 => 1+2+b=3+b chia hết cho 3
=> b=0,3,6,9
Số cần tìm là: 10, 13, 16 và 19
7 tháng 3 2018
Số lớn nhất có hai chữ số chia hết cho 2 là : 98
Số bé nhất có hai chữ số chia hết cho 2 là : 10
Có tất cả: ( 98 - 10 ) : 2 + 1 = 45 (số chia hết cho 2 )
Đáp số : 45 số
11 tháng 11 2019
Gọi số cần tìm là ab.
Ta có : ab = ba - 63
=> 10a + b = 10b + a - 63
=> 9a = 9b - 63
=> 9b - 9a = 63
=> 9. (b - a) = 63
=> b - a = 7
Ta lại có : b + a = 9
=> b = (7 + 9) : 2 = 8
=> a = 8 - 7 = 1
Vậy số cần tìm là 18.
XU
2
TA
2 tháng 3 2021
Gọi số cần tìm là `\overline(ab)`
Tổng 2 chữ số là 10 `=> a+b=10`
Tích 2 chữ số nhỏ hơn số đã cho là 12 `=> a.b+12=\overline(ab)=10a+b`
Ta có hệ: $\begin{cases}a+b=10\\ab+12=10a+b\\\end{cases}$
Giải hệ ta được: $\begin{cases}a=2\\b=8\\\end{cases}$
Vậy `\overline(ab)=28`.
4 tháng 2 2021
Gọi số phải tìm có dạng là ab(Có dấu gạch ngang trên đầu)(Điều kiện: \(a,b\in N\); \(0< a< 10\); \(1\le b< 10\))
Vì tổng 2 chữ số là 10 nên ta có phương trình: a+b=10(1)
Vì tích 2 chữ số ấy nhỏ hơn số đã cho là 12 nên ta có phương trình: \(ab+12=10a+b\)(2)
Từ (1) và (2) ta lập được hệ phương trình
\(\left\{{}\begin{matrix}a+b=10\\ab+12=10a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=10-a\\a\left(10-a\right)+12=10a+10-a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=10-a\\10a-a^2+12-9a-10=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a^2+a+2=0\\b=10-a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2-a-2=0\\b=10-a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(a-2\right)\left(a+1\right)=0\\b=10-a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=10-2=8\end{matrix}\right.\)(thỏa ĐK)
Vậy: Số cần tìm là 28
A
4 tháng 2 2021
Gọi số cần tìm là \(\dfrac{ }{ab}\) (điều kiện bạn tự viết nhé)
Vì tổng 2 chữ số là 10 nên ta có:
\(a+b=10\) (1)
⇔\(b=10-a\)
Vì tích 2 chữ số nhỏ hơn số đã cho 12 nên:
\(a.b+12=10a+b\) (2)
Thay (1) vào (2) ta được:
\(a\left(10-a\right)+12=10a+10-a\)
⇔\(10a-a^2+12=9a+10\)
⇔\(-a^2+a+2=0\)
⇔\(\left(a+1\right)\left(2-a\right)=0\)
⇔\(\left[{}\begin{matrix}a+1=0\\2-a=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}a=-1\\a=2\end{matrix}\right.\)
Mà \(a\in N,a\ne0\)
⇒\(a=2\)
⇒\(b=10-a=10-2=8\)
Vậy số cần tìm là 28
