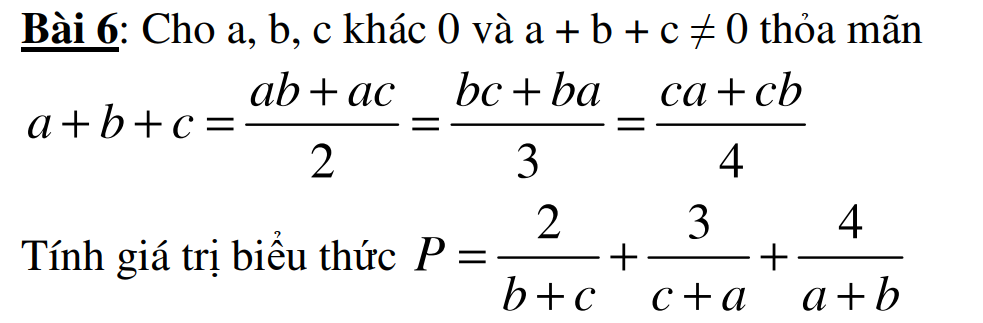
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak. mình sẽ tick
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
0
NK
0
NK
2
15 tháng 9 2021
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{2\left(a+b+c\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}b+c=2a\\c+a=2b\\a+b=2c\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}=\dfrac{2a}{a}+\dfrac{2b}{b}+\dfrac{2c}{c}=2+2+2=6\)
S
15 tháng 9 2021
P=
\(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}=\dfrac{a}{b+c}.\left(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\right):\left(\dfrac{a}{b+c}\right)=\left(\dfrac{b+c}{a}.\dfrac{a}{b+c}+\dfrac{c+a}{b}.\dfrac{a}{b+c}+\dfrac{a+b}{c}.\dfrac{a}{b+c}\right):\dfrac{a}{b+c}=\left(\dfrac{b+c}{a}.\dfrac{a}{b+c}+\dfrac{c+a}{b}.\dfrac{b}{c+a}+\dfrac{a+b}{c}.\dfrac{c}{a+b}\right):\dfrac{a}{b+c}=\left(1+1+1\right):\dfrac{a}{b+c}=3.\dfrac{b+c}{a}=\dfrac{3b+3c}{a}\)
NK
1
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Lời giải:
Bổ sung điều kiện $a,b,c$ không thể đồng thời bằng $0$
Từ đkđb suy ra:
\(\frac{6(10a-15b)}{2007.6}=\frac{15(6b-10c)}{15.2008}=\frac{10(15c-6a)}{10.2009}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{6(10a-15b)}{2007.6}=\frac{15(6b-10c)}{15.2008}=\frac{10(15c-6a)}{10.2009}=\frac{6(10a-15b)+15(6b-10c)+10(15c-6a)}{2007.6+15.2008+10.2009}=0\)
\(\Rightarrow 10a-15b=6b-10c=15c-6a=0\)
\(\Leftrightarrow 10a=15b; 6b=10c; 15c=6a\Leftrightarrow \frac{a}{15}=\frac{b}{10}=\frac{c}{6}\)
Đặt $\frac{a}{15}=\frac{b}{10}=\frac{c}{6}=k$ thì: $a=15k, b=10k, c=6k$
Vì $a,b,c$ không thể đồng thời bằng $0$ nên $k\neq 0$
Khi đó:
$P=\frac{15k.10k+10k.6k+15k.6k}{(15k)^2+(10k)^2+(6k)^2}$
$=\frac{300k^2}{361k^2}=\frac{300}{361}$
NK
1
15 tháng 9 2021
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{2\left(a+b+c\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}2a=b+c\\2b=a+c\\2c=a+b\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{\left(a+b\right)^3}{c^3}+\dfrac{\left(b+c\right)^3}{a^3}+\dfrac{\left(c+a\right)^3}{b^3}=\left(\dfrac{a+b}{c}\right)^3+\left(\dfrac{b+c}{a}\right)^3+\left(\dfrac{c+a}{b}\right)^3=\left(\dfrac{2c}{c}\right)^3+\left(\dfrac{2a}{a}\right)^3+\left(\dfrac{2b}{b}\right)^3=2^3+2^3+2^3=24\)
NK
1
15 tháng 9 2021
Áp dụng t/c dãy tỉ số bằng nhau
\(\dfrac{a}{2013}=\dfrac{b}{2012}=\dfrac{c}{2011}=\dfrac{a-c}{2}=\dfrac{a-b}{1}=\dfrac{b-c}{1}\\ \Rightarrow a-c=2\left(a-b\right)=2\left(b-c\right)\)
\(\Rightarrow H=\dfrac{\left[2\left(a-b\right)\right]^4}{\left(a-b\right)^2\left(a-b\right)^2}=\dfrac{16\left(a-b\right)^4}{\left(a-b\right)^4}=16\)
TT
1
12 tháng 8 2021
từ điểm B kẻ \(Bz//Cy=>\angle\left(BCy\right)+\angle\left(CBz\right)=180^o\)(góc trong cùng phía)
\(=>\angle\left(CBz\right)=180^o-130^o=50^o\)
\(=>\angle\left(ABz\right)=\angle\left(ABC\right)+\angle\left(CBz\right)=50^o+72^o=122^o\)
\(=>\angle\left(BAx\right)+\angle\left(ABz\right)=180^o\)
mà 2 góc này ở vị trí trong cùng phía
\(=>Ax//Bz=>Ax//Cy\)
