Chứng minh rằng: nếu 1 tam giác có 2 đường trung tuyến vuông góc với nhau thì tổng các bình phương của 2 đường trung tuyến này bằng bình phương của đường trung tuyến thứ ba.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 3 2015
theo đề ta ta có BM2+AH2+CN2 = 3/2 AC2.
ta có trong tam giác vuông đường trung tuyến cắt cạnh huyền bằng 1/2 cạnh huyền từ đó suy ra BM2=1/2 AC2 (1)
ta có: AH2 = AB2 +BH2 (vì tam giác ABH vuông tại B) = AB2+ (1/2BC)2=AB2+1/4BC2 (do AH là trung tuyến BC) (2)
tương tự ta có CN2= BC2 +BN2=BC2+1/4AB2 (3)
lấy (2)+(3) ta có AB2+1/4BC2+BC2+1/4AB2=5/4 AB2+5/4 BC2 = 5/4 AC2(4)
lấy (1)+(4) đó chính là điều ta cần chứng minh
16 tháng 11 2016
Kẻ AH vuông với BC
==
===
\(\Rightarrow\) \(\frac{2\left(AC^2+AB^2\right)-BC^2}{4}=AH^2+HM^2\)= AM2
\(\Rightarrow\)dpcm
29 tháng 4 2018
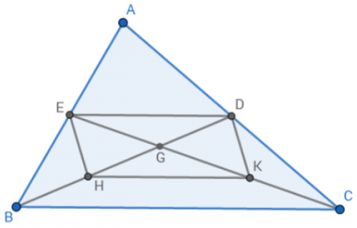
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi
Giả sử \(\Delta\)ABC có hai đường trung tuyến BE và CF vuông góc với nhau, AD là đường trung tuyến thứ ba. Ta cần chứng minh AD^2 = BE^2 + CF^2
Trên tia đối của tia EF lấy điểm K sao cho EF = FK
Tứ giác AKCF có hai đường chéo cắt nhau tại trung điểm E của mỗi đường nên AKCF là hình bình hành => AK//FC. Mà FC\(\perp\)BE nên BE\(\perp\)AK (*)
Ta có: F là trung điểm của AB, E là trung điểm của AC nên EF là đường trung bình của\(\Delta\)ABC => EF = 1/2BC và EF//BC hay EK//BD (1)
Mà BD = 1/2BC (gt) nên EF = BD => EK = BD (do EF = EK theo cách chọn điểm phụ) (2)
Từ (1) và (2) suy ra EKDB là hình bình hành => EB // DK (**)
Từ (*) và (**) suy ra DK \(\perp\)AK => \(\Delta\)AKD vuông tại K => AK^2 + KD^2 = AD^2 (theo định lý Py-ta-go)
Mà AK = FC (do AKCF là hình bình hành) và KD = BE (do EKDB là hình bình hành) nên AD^2 = BE^2 + CF^2 (đpcm)