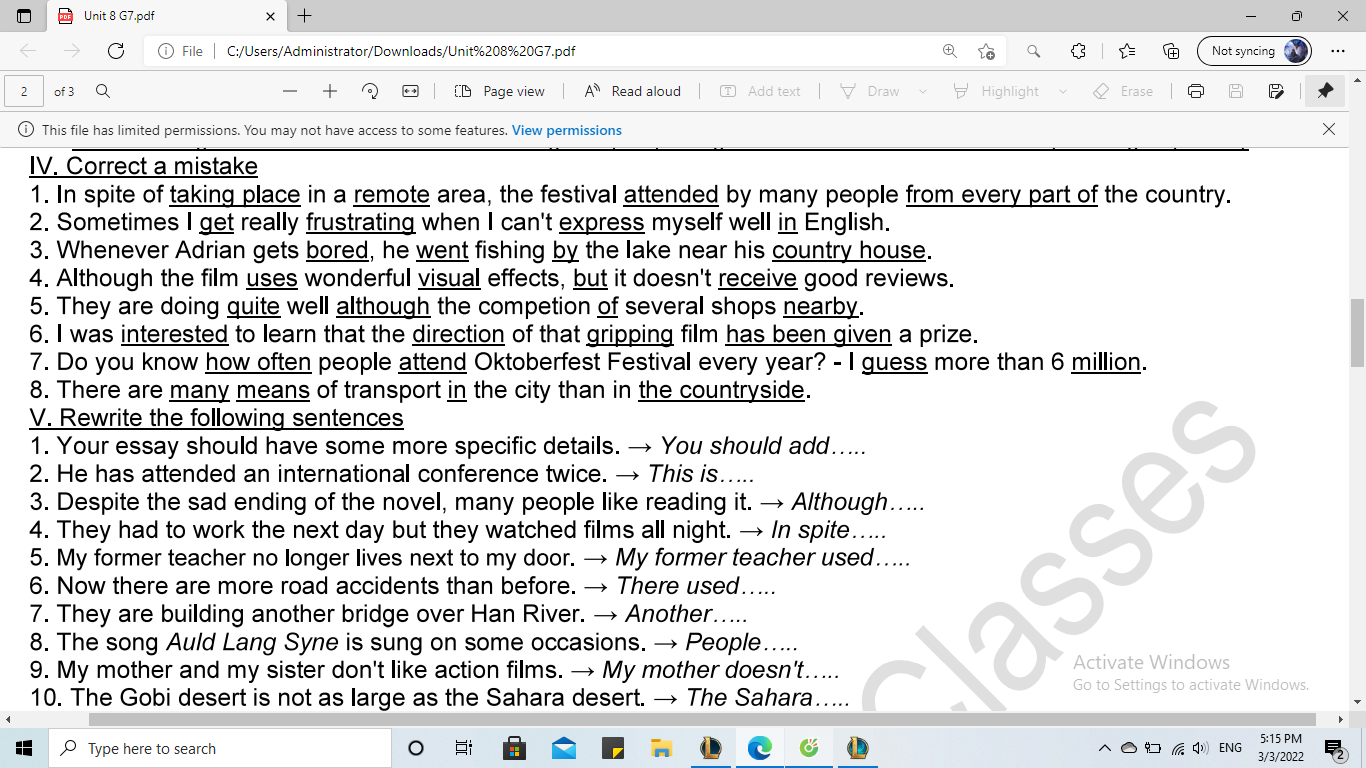
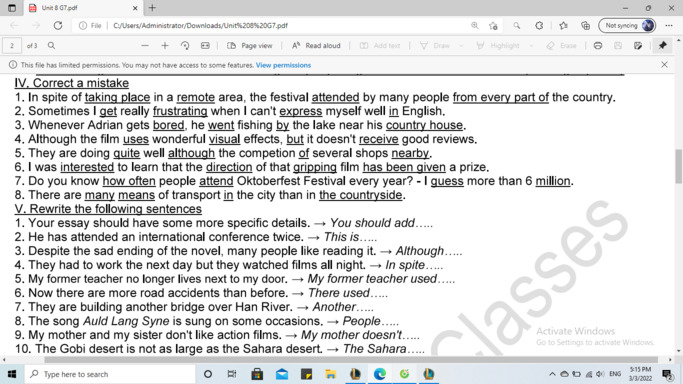
bài nào cũng đc ạ:33
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Bài 1.1
a. Để căn thức có nghĩa (CTCN) thì $2x-1\geq 0$
$\Leftrightarrow x\geq \frac{1}{2}$
b. Để CTCN thì $-2x+0,5\geq 0$
$\Leftrightarrow 0,5\geq 2x\Leftrightarrow x\leq \frac{1}{4}$
c. Để CTCN thì \(\left\{\begin{matrix} x-1\neq 0\\ \frac{1}{x-1}\geq 0\end{matrix}\right.\Leftrightarrow x-1>0\Leftrightarrow x>1\)
d. Để CTCN thì \(\left\{\begin{matrix} x^2+2021\neq 0\\ \frac{2022-x}{x^2+2021}\geq 0\end{matrix}\right.\Leftrightarrow 2022-x\geq 0\) (do $x^2+2021>0$ với mọi $x\in\mathbb{R}$)
$\Leftrightarrow x\leq 2022$
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Bài 1.2
a. $3=\sqrt{9}>\sqrt{8}$
b. $-7=-\sqrt{49}> -\sqrt{51}$
c. $3+\sqrt{2}> 3+\sqrt{1}=4=2+2=2+\sqrt{4}> 2+\sqrt{3}$
d. $\sqrt{26}+3>\sqrt{25}+3=8=\sqrt{64}>\sqrt{63}$
e.
$\frac{1}{2}=\frac{2-1}{2}=\frac{\sqrt{4}-1}{2}> \frac{\sqrt{2}-1}{2}$
f.
Xét hiệu $5-2\sqrt{7}-(3-\sqrt{10})=2-(\sqrt{28}-\sqrt{10})$
$=2-\frac{18}{\sqrt{28}+\sqrt{10}}< 2-\frac{18}{\sqrt{2(28+10)}}$ (áp dụng BĐT $\sqrt{a}+\sqrt{b}\leq \sqrt{2(a+b)}$)
$=2-\frac{18}{\sqrt{76}}< 2-\frac{18}{\sqrt{81}}=0$
$\Rightarrow 5-2\sqrt{7}< 3-\sqrt{10}$
CN
0
K
13 tháng 12 2020
11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
K
13 tháng 12 2020
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)
