phân tích đa thức thành nhân tử :(x-y)^3+(y-2)^3+(2-x)^3 x^2*y*z*(y-z)+y^2*z^2*(z-y) x^3+y^3+z^3-3*x*y*z
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
VX
10 tháng 11 2021
x(y+z)^2 - y(z-x)^2 +z(x+y)^2 - x^3 + y^3 - z^3 - 4xyz
=xy^2+2xyz+xz^2-yz^2+2xyz-x^2y+x^2z+2xyz+zy^2-x^3+y^3-z^3-4xyz
=xy^2+xz^2-yz^2-x^2y+x^2z+y^2z-x^3+y^3-z^3+2xyz
=(xy^2+2xyz+xz^2)-x^3-(yz^2+2xyz+x^2y)+y^3+(x^2z+2xyz+y^2z)-z^3
=x[(y+z)^2-x^2)-y[(z+x)^2-y^2]+z[(x+y)^2-z^2]
=x(-x+y+z)(x+y+z)-y(x-y+z)(x+y+z)+z(x+y-z)(x+y+z)
=(x+y+z)[-x^2+xy+xz-xy+y^2-yz+xz+yz-z^2]
=(x+y+z)[-x(x-y-z)-y(x-y-z)+z(x-y-z)]
=(x+y+z)(x-y-z)(z-x-y)
HT
1
VX
10 tháng 11 2021
x(y+z)^2 - y(z-x)^2 +z(x+y)^2 - x^3 + y^3 - z^3 - 4xyz
=xy^2+2xyz+xz^2-yz^2+2xyz-x^2y+x^2z+2xyz+zy^2-x^3+y^3-z^3-4xyz
=xy^2+xz^2-yz^2-x^2y+x^2z+y^2z-x^3+y^3-z^3+2xyz
=(xy^2+2xyz+xz^2)-x^3-(yz^2+2xyz+x^2y)+y^3+(x^2z+2xyz+y^2z)-z^3
=x[(y+z)^2-x^2)-y[(z+x)^2-y^2]+z[(x+y)^2-z^2]
=x(-x+y+z)(x+y+z)-y(x-y+z)(x+y+z)+z(x+y-z)(x+y+z)
=(x+y+z)[-x^2+xy+xz-xy+y^2-yz+xz+yz-z^2]
=(x+y+z)[-x(x-y-z)-y(x-y-z)+z(x-y-z)]
=(x+y+z)(x-y-z)(z-x-y)
NH
2
2 tháng 8 2021
\(z^3\left(x+y^2\right)+y^3\left(z-x^2\right)-x^3\left(y+z^2\right)-xyz\left(xyz-1\right)\)
\(=xz^3+y^2z^3+y^3z-x^2y^3-x^3-x^3z^2-x^2y^2z^2+xyz\)
\(=\left(y^2z^3+y^3z\right)+\left(xz^3+xyz\right)-\left(x^2y^3+x^2y^2z^2\right)-x^3\left(y+z^2\right)\)
\(=y^2z\left(y+z^2\right)+xz\left(y+z^2\right)-x^2y^2\left(y+z^2\right)-x^3\left(y+z^2\right)\)
\(=\left(y+z^2\right)\left(y^2z+xz-x^2y^2-x^3\right)\)
\(=\left(y+z^2\right)\left[z\left(y^2+x\right)-x^2\left(y^2+x\right)\right]\)
\(=\left(y+z^2\right)\left(z-x^2\right)\left(y^2+x\right)\)
Tick hộ nha bạn 😘
G
1
VX
10 tháng 11 2021
x(y+z)^2 - y(z-x)^2 +z(x+y)^2 - x^3 + y^3 - z^3 - 4xyz
=xy^2+2xyz+xz^2-yz^2+2xyz-x^2y+x^2z+2xyz+zy^2-x^3+y^3-z^3-4xyz
=xy^2+xz^2-yz^2-x^2y+x^2z+y^2z-x^3+y^3-z^3+2xyz
=(xy^2+2xyz+xz^2)-x^3-(yz^2+2xyz+x^2y)+y^3+(x^2z+2xyz+y^2z)-z^3
=x[(y+z)^2-x^2)-y[(z+x)^2-y^2]+z[(x+y)^2-z^2]
=x(-x+y+z)(x+y+z)-y(x-y+z)(x+y+z)+z(x+y-z)(x+y+z)
=(x+y+z)[-x^2+xy+xz-xy+y^2-yz+xz+yz-z^2]
=(x+y+z)[-x(x-y-z)-y(x-y-z)+z(x-y-z)]
=(x+y+z)(x-y-z)(z-x-y)
LP
1
5 tháng 9 2021
tham khảo:https://hoc247.net/hoi-dap/toan-8/phan-tich-da-thuc-x-2-y-2-3-z-2-x-2-3-y-2-z-2-3-thanh-nhan-tu-faq358831.html
TN
2
11 tháng 7 2021
Đây bạn nhé
Bạn làm theo người này nhé, mik cũng khum bt. mik chỉ nhắc để bn có đáp án nhanh nhất thui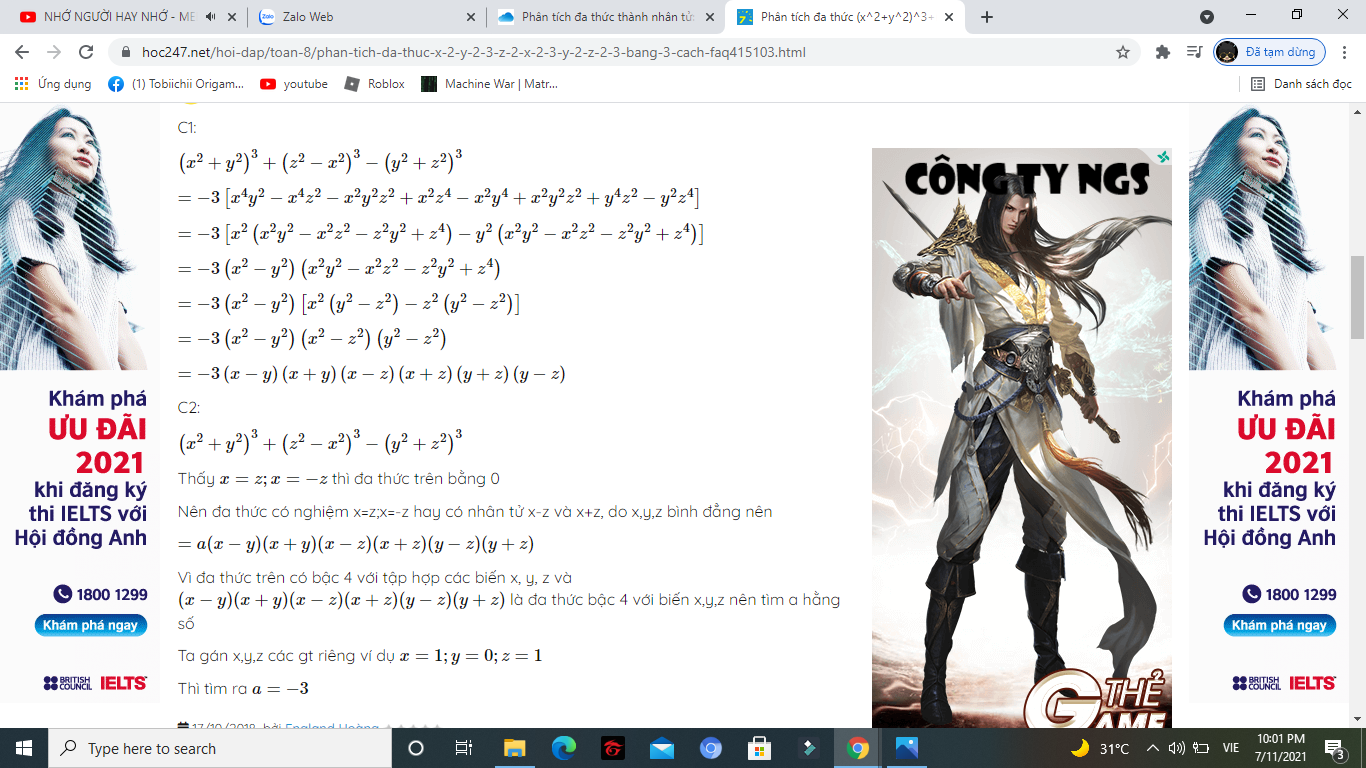 
21 tháng 1 2022
b: \(=\dfrac{12\left(y-z\right)^4+3\left(y-z\right)^5}{6\left(y-z\right)^2}=2\left(y-z\right)^2+\dfrac{1}{2}\left(y-z\right)^3\)
PH
0
CM
17 tháng 11 2019
a) (x - 1)(x + l)(x - 2)(x - 4). b) (x - 2)( x 2 + 4).
c) 2y(3 x 2 + y 2 ). d) 2(x + y + z) ( a - b ) 2 .
24 tháng 8 2021
a. \(x^2\left(x-3\right)^2-\left(x-3\right)^2-x^2+1\)
\(=\left(x-3\right)^2\left(x^2-1\right)-\left(x^2-1\right)\)
\(=\left[\left(x-3\right)^2-1\right]\left(x^2-1\right)\)
\(=\left(x-3+1\right)\left(x-3-1\right)\left(x+1\right)\left(x-1\right)\)
\(=\left(x-2\right)\left(x-4\right)\left(x+1\right)\left(x-1\right)\)
b. \(x^3-2x^2+4x-8\)
\(=\left(x^3+4x\right)-\left(2x^2+8\right)\)
\(=x\left(x^2+4\right)-2\left(x^2+4\right)\)
\(=\left(x-2\right)\left(x^2+4\right)\)
c. \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=\left(x^3+3x^2y+3xy^2+y^3\right)-\left(x^3-3x^2y+3xy^2-y^3\right)\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3\)
\(=2y\left(3x^2+y^2\right)\)
d. \(2a^2\left(x+y+z\right)-4ab\left(x+y+z\right)+2b^2\left(x+y+z\right)\)
\(=\left(2a^2-4ab+2b^2\right)\left(x+y+z\right)\)
\(=2\left(a^2-2ab+b^2\right)\left(x+y+z\right)\)
\(=2\left(a-b\right)^2\left(x+y+z\right)\)
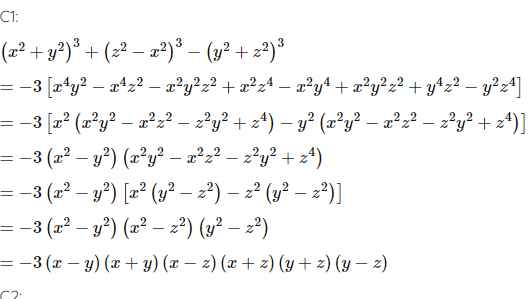
\(x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+z^3-3xyz\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-\left(x+y\right)z+z^2\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\)
Bài 3)
Ta có :
\(x^3+y^3+z^3-3xyz\)
\(\Rightarrow\left(x+y\right)^3-3xy\left(x+y\right)+z^3-3xyz\)
\(\Rightarrow\left(x+y+z\right)\left[\left(x+y^2\right)-\left(x+y\right)z+z^2\right]-3xy\left(x+y+z\right)\)
\(\Rightarrow\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\)
P/s tham khảo nha
hok tốt