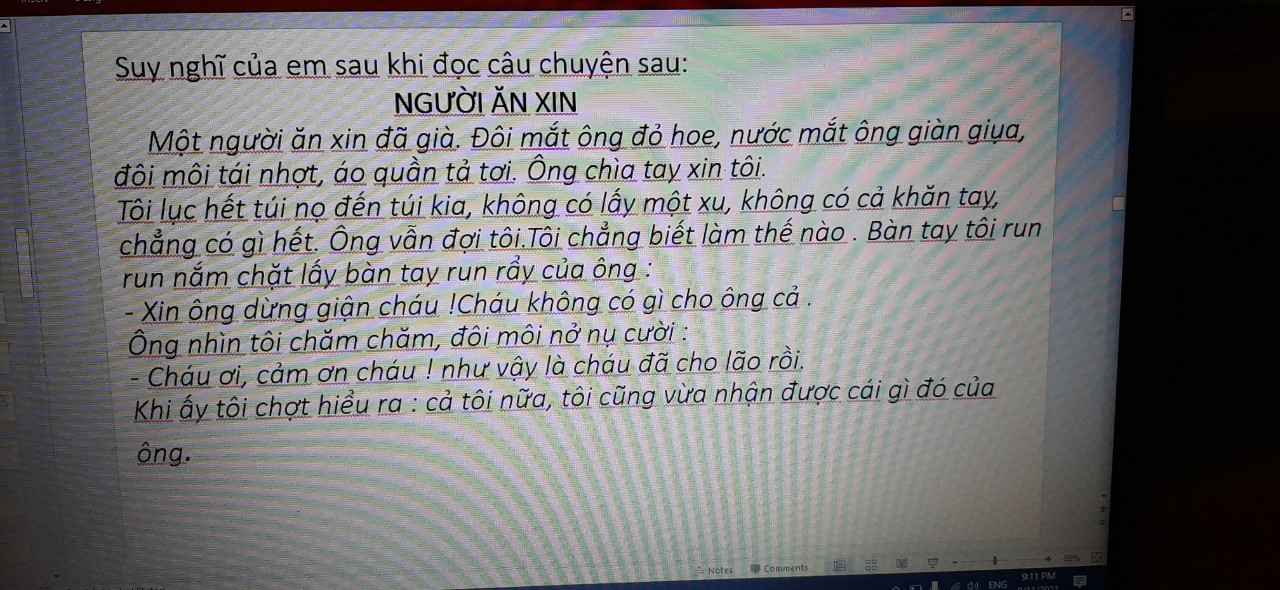
mọi người ơi giúp mik với giúp mik mik tick cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{2021a}{2021b}=\dfrac{2021a-c}{2021b-d}\)
c, Ta có \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\left(\dfrac{a}{b}\right)^2=\left(\dfrac{c}{d}\right)^2\)
Áp dụng t/c dtsbn:
\(\left(\dfrac{a}{b}\right)^2=\left(\dfrac{c}{d}\right)^2=\dfrac{a^2}{b^2}=\dfrac{c^2}{d^2}=\dfrac{a^2+c^2}{b^2+d^2}\)



Ta có: Bt là tia p/g của \(\widehat{ABC}\)
\(\Rightarrow\widehat{ABt}=\widehat{CBt}=\dfrac{\widehat{ABC}}{2}=80^0:2=40^0\)
Ta lại có: \(\widehat{BAx}=\widehat{ABt}=40^0\) (so le trong)
⇒Bt//Ax
Kẻ Ca là tia đối của Cy
Lại có: \(\widehat{BCa}\) kề bù với \(\widehat{BCy}\)
\(\Rightarrow\widehat{BCa}+\widehat{BCy}=180^0\)
\(\Rightarrow\widehat{BCa}+40^0=180^0\)
\(\Rightarrow\widehat{BCa}=140^0\)
Mà \(\widehat{CBt}=\widehat{BCa}=40^0\) và 2 góc này so le trong
Ca//Bt hay Cy//Bt
ôi cảm ơn bạn nhoa !!!
chúc bạn một buổi tối tốt lành :>>>


11)\(\dfrac{3x+1}{x-5}+\dfrac{2x}{x-5}=\dfrac{3x+2x+1}{x-5}=\dfrac{5x+1}{x-5}\)
12)\(\dfrac{4-x^2}{x-3}+\dfrac{2}{x^2-9}=\dfrac{4-x^2}{x-3}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{\left(4-x^2\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{2+\left(2-x\right)\left(2+x\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
13)
\(\dfrac{3}{4x-2}+\dfrac{2x}{4x^2-1}=\dfrac{3}{2\left(2x-1\right)}+\dfrac{2x}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{3\left(2x+1\right)}{2\left(2x-1\right)\left(2x+1\right)}+\dfrac{2.2x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{6x+3+4x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{10x+3}{2\left(2x-1\right)\left(2x+1\right)}\)
14)
\(\dfrac{2x+1}{2x-4}+\dfrac{5}{x^2-4}=\dfrac{2x+1}{2\left(x-2\right)}+\dfrac{5}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(2x+1\right)\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\dfrac{5.2}{2\left(x-2\right)\left(x+2\right)}=\dfrac{2x^2+5x+12}{2\left(x-2\right)\left(x+2\right)}\)