Cho tam giác ABC cố định, trên BC lấy điểm I thay đổi. Tìm tập hợp điểm M thoả vectoIM=vectoIA+vectoIC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
6 tháng 8 2018
b) Dựng hình bình hành ABCD
Tam giác ABC đều:
Kẻ BH⊥AC ⇒BD⊥AC
Tam giác HAB vuông tại H:
BH=AB.sinA=a.sin60=\(\dfrac{a\sqrt{3}}{2}\)
BD=2AH=\(2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
Vecto v=vectoBA+vectoBC=vectoBD
|vecto v|=|vectoBD|=BD=\(a\sqrt{3}\)
CH
Cô Hoàng Huyền
Admin
VIP
27 tháng 9 2017
a) Xét tam giác DBI và tam giác BAH có:
\(\widehat{DIB}=\widehat{BHA}=90^o\)
BD = AB (Tam giác ABD vuông cân tại B)
\(\widehat{DBI}=\widehat{BAH}\) (Cùng phụ với góc ABH)
Vậy nên \(\Delta DBI=\Delta BAH\)(Cạnh huyền góc nhọn)
\(\Rightarrow DI=BH.\)
Tương tự ta chứng minh được EK = CH.
b) Gọi J là trung điểm DE. Do DI và EK cùng vuông góc bới BC nên chúng song song nhau.
Từ J kẻ, JM // DI // EK. Khi đó \(JM\perp BC.\)
Xét hình thang DIKE ta thấy ngay JM chính là đường trung bình của hình thang. Vậy M là trung điểm IK.
Lại có theo câu a, \(\Delta DBI=\Delta BAH\Rightarrow IB=AH\), tương tự KC = AH.
Vậy thì MB = MC hay JM là đường trung tuyến tam giác JBC.
Vậy thì \(JM=\frac{DI+EK}{2}=\frac{BH+CH}{2}=\frac{BC}{2}\)
Xét tam giác JBC có đường trung tuyến bằng một nửa cạnh huyền nên nó là tam giác vuông. Lại có JM đồng thời là đường cao nên tam giác JBC vuông cân tại J. Do BC cố định nên J cố định.
Vậy DE luôn đi qua một điểm cố đỉnh, là đỉnh J nằm cùng phía A so với BC và thỏa mãn tam giác JBC vuông cân tại J.
28 tháng 3 2020
Hình nếu chị không vẽ được thì hỏi em nhé chị !
Gọi I là trung điểm của BC => I cố định ( vì B,C cố định )
Ta có : AG = 2.OI ( theo bổ đề 7 )
Lại có AM = AH nên AM = 2.OI ( 1 )
Trên tia IO lấy điểm K sao cho OK = 2. OI ( 2 )
=> K cố định ( vì O,I cố định )
Từ ( 1 ) ( 2 ) => AM = KO mà AM// KO
( vì cùng vuông góc với BC ) .
Do đó AMKO là hình bình hành nên KM = OA = R : không đổi
Vậy khi A thay đổi trên cung lớn BC thì điểm M đi động trên đường tròn cố định ( K ; R ) => đpcm
CM
25 tháng 6 2019
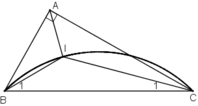
* Dự đoán : Quỹ tích điểm I là cung chứa góc 135 º dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc 135 º dựng trên đoạn BC.
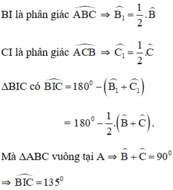
⇒ I thuộc cung chứa góc 135 º dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc 135 º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135 º dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của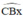 
+ Kẻ tia Cy sao cho CI là phân giác của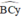 
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
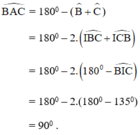
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận : Quỹ tích điểm I là toàn bộ cung chứa góc 135 º dựng trên đoạn BC (khác B và C).
Kiến thức áp dụng
+ Thông thường, bài toán quỹ tích ta làm theo các bước :
1, Dự đoán quỹ tích
2, Chứng minh quỹ tích : gồm Phần thuận và Phần đảo
3, Kết luận.
+ Quỹ tích các điểm M thỏa mãn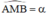 
(với A, B cố định, α không đổi) là cung chứa góc α dựng trên đoạn AB. (Cách dựng xem SGK).
CM
17 tháng 6 2019
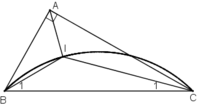
* Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc 135º dựng trên đoạn BC.
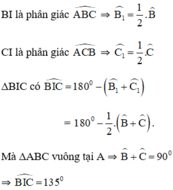
⇒ I thuộc cung chứa góc 135º dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của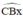 
+ Kẻ tia Cy sao cho CI là phân giác của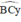 
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
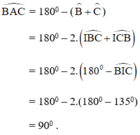
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận : Quỹ tích điểm I là toàn bộ cung chứa góc 135º dựng trên đoạn BC (khác B và C).
CM
2 tháng 8 2019
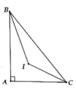
Tương tự câu 1
Tính được B I C ^ = 135 0
=> Quỹ tích của điểm I là hai cung chứa góc 135 0 dựng trên đoạn BC
