cho 5 điểm phân biệt a,b,c,d,e.kể tên các vectơ khác vectơ không được tạo thành từ 5 điểm trên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các vectơ khác vectơ – không được lập ra từ 4 điểm đã cho là:
A B → ; A C → ; A D → ; B A → ; B C → ; B D → ; C A → ; C B → ; C D → ; D A → ; D B → ; D C →
Đáp án C


Xét tập X = {A, B, C, D, E ; F}. Với mỗi cách chọn hai phần tử của tập X và sắp xếp theo một thứ tự ta được một vectơ thỏa mãn yêu cầu
Mỗi vectơ thỏa mãn yêu cầu tương ứng cho ta một chỉnh hợp chập 2 của 6 phần tử thuộc tập X.
Vậy số các vectơ thỏa mãn yêu cầu bằng số tất cả các chỉnh hợp chập 2 của 6, bằng
Chọn C.

a, tia AB,AC,AD,AE
BC,BD;BE
CD,CE
DE
\(\Rightarrow\)CÓ 10 tia.
b,theo đề bài ta có:
\(\frac{n\times\left(n-1\right)}{2}=132\)
\(\Leftrightarrow n\times\left(n-1\right)=264\)
\(\Rightarrow n\times\left(n-1\right)=\)
hình như đề bj sai bn ạ !sửa 132 tia của đề thành 66 tia thì n=12 nha
sau khi sửa đề nè bn:
:\(\frac{n\times\left(n-1\right)}{2}=66\)
\(\Leftrightarrow n\times\left(n-1\right)=132\)
\(\Leftrightarrow n\times\left(n-1\right)=12\times11\)
\(\Rightarrow n=12\)

Đáp án B.
Từ 2 điểm phân biệt có thể tạo được 2 vecto nên số vecto tạo ra được là ![]()

Đáp án B.
Từ 2 điểm phân biệt có thể tạo được 2 vecto nên số vecto tạo ra được là A 10 2 .
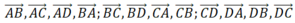
Lời giải:
$\overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AD}, \overrightarrow{AE}$
$\overrightarrow{BA}, \overrightarrow{BC}, \overrightarrow{BD}, \overrightarrow{BE}$
$\overrightarrow{CA}, \overrightarrow{CB}, \overrightarrow{CD}, \overrightarrow{CE}$
$\overrightarrow{DA}, \overrightarrow{DB}, \overrightarrow{DC}, \overrightarrow{DE}$
$\overrightarrow{EA}, \overrightarrow{EB}, \overrightarrow{EC}, \overrightarrow{ED}$