Một chất điểm dao động điều hòa có vận tốc cực đại 60cm/s và gia tốc cực đại là 2pi. Chọn mốc thế năng tại vị trí cân bằng. Thời điểm ban đầu t=0, chất điewmr có v=30cm/s và thế năng đang tăng. Chất đuêmr có a=pi lần đầu ở thời điểm??
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
18 tháng 7 2018
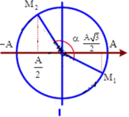
v max = ω A = 0 , 60 m / s a max = ω 2 A = 2 π m / s 2 ⇒ ω = a max v max = 2 π 0 , 6 = 10 π 3 r a d / s T = 2 π ω = 0 , 6 s
+ Khi t = 0 ; v 0 = 30 c m / s = + v max 2
⇒ x 0 = A 2 − v 0 2 ω 2 = A 2 − ω A 2 2 ω 2 = ± A 3 2
+ Khi đó, thế năng của vật đang tăng và vật chuyển động theo chiều dương nên x = + A 3 2
+ Khi vật có gia tốc bằng li độ bằng π m / s 2 = a max 2 thì li độ vật là x: x A = − a a max = − 1 2 ⇒ x = − A 2
+ Chất điểm có gia tốc bằng π (m/s2) lần đầu tiên ở thời điểm:
t = α 2 π . T = π 6 + π 2 + π 6 2 π T = 5 12 T = 5 12 .0 , 6 = 0 , 25 s
Chọn đáp án D
VT
31 tháng 8 2017
Đáp án D
v m a x = ω A = 0 , 6 ( m / s ) ; a m a x = ω 2 A = 2 π ( m / s 2 )
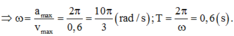
Khi t = 0, v 0 = 30 cm/s = + v m a x
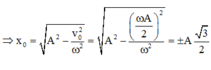
Khi đó, thế năng của vật đang tăng và vật chuyển động theo chiều dương nên x 0 = + A 3 2 .
Khi vật có gia tốc bằng π ( m / s 2 ) = a m a x 2 thì li độ của vật là x:
Chất điểm có gia tốc bằng π ( m / s 2 ) lần đầu tiên ở thời điểm:
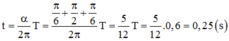
Vmax=\(\omega\).A=60, . amax=\(\omega\).\(\omega\).A=2π => \(\omega\)=\(\dfrac{ }{ }\)π/30,=>A=1800/π.
Tại t=0, v=-\(\omega\).A. sin(\(\varphi\))=>sin(\(\varphi\))=-0,5.mà v>0=>x<0=>cos(\(\varphi\))=-\(\sqrt{ }\)3/2=>x=-(1800/π).\(\sqrt{ }\)3/2=-A.\(\sqrt{ }\)3/2.
a=-\(\omega\).\(\omega\).x=>x=-900/π=-A/2.
=>Chất điểm qua a=2π tại thoi điểm t=T/12 + T/6=T/4=> t =15s
Đính chính a=π,\(\omega\) không có âm