Cho tam giác ABC. Gọi d là đường phân giác của góc ngoài ở đỉnh A. Trên đường thẳng d lấy điểm M (M khác A). CMR: BA + AC < BM + MC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trên tia đối của tia AC lấy điểm D sao cho AB = AD
=> AB + AC = AD + AC
Tam giác AMD = tam giác AMB ( c.g.c )
=> MD = MB ( 2 cạnh tương ứng )
=> MB + MC = MD + MC
Xét tam giác MCD theo bđt tam giác ta có
MD + MC > CD
=> MB + MC > AB + AC ( đpcm )

Xét (O) có
ΔCDM nội tiếp
CM là đường kính
DO đó: ΔCDM vuông tại D
Xét tứ giác ABCD có
\(\widehat{CDB}=\widehat{CAB}=90^0\)
Do đó: ABCD là tứ giác nội tiếp
b: \(\widehat{BCA}=\widehat{ADB}\)
mà \(\widehat{ADB}=\widehat{KCA}\)
nên \(\widehat{BCA}=\widehat{KCA}\)
hay CA là tia phân giác của góc KCB

a) ΔABDΔABD cân tại A => BADˆ=BDAˆBAD^=BDA^ (t/c tam giác cân)
Lại có: BADˆ+DAEˆ=BACˆ=90oBAD^+DAE^=BAC^=90o
BDAˆ+ADEˆ=BDEˆ=90oBDA^+ADE^=BDE^=90o
Do đó, DAEˆ=ADEˆDAE^=ADE^
=> ΔADEΔADE cân tại E (dấu hiệu nhận biết tam giác cân)
=> AE = ED (t/c tam giác cân) (đpcm)
b) Có: AH // ED (cùng ⊥BC⊥BC)
=> HADˆ=ADEˆHAD^=ADE^ (so le trong)
= DAE (câu a)
=> AD là phân giác HACˆ(đpcm)
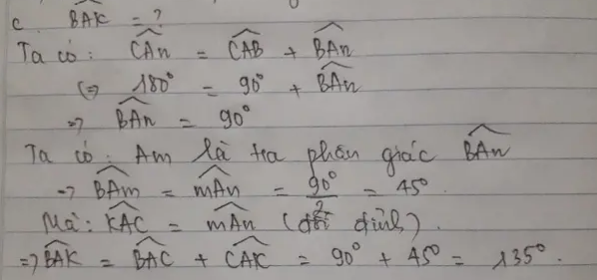
Hình bạn tự vẽ nhé
Trước tiên từ C kẻ đường vuông góc với đường thẳng d và vắt AB tại A'
Từ đó chứng minh được: A'M=MC và A'A=AC
Kẻ M với B
Theo bài ra, ta có trong tam giác MBA' có:
MC+MB>BA' (1)
Mà BA'=BA+AA' = BA + AC (2)
Từ (1) và (2) suy ra BA + AC < BM + MC
Chúc bạn học tốt
Bình chọn cho mình nhé