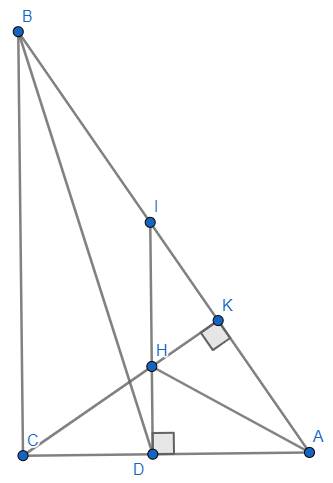
Cho △ABC có 3 góc nhọn. Kẻ đường cao BD và CE cắt nhau tại H. Nối AH cắt BC ở I.
1) Chứng minh AI ⊥ BC.
2) Chứng minh ∠BAI = ∠BCE.
3) Kẻ Bx ⊥ BA; Cy ⊥ AC; Bx giao với Cy tại M. Gọi O là trung điểm của BC. Chứng minh BH = CM và 3 điểm H,O,M thẳng hàng.
4) Chứng minh BM = CH.
5) Giả sử ∠BAC = 50o, xác định số đo của ∠BHC.
~~ GIÚP VỚI CÁC BẠN !!!!! Mình đang vô vùng gấp gáp !!!!!!
~~ Mình cảm ơn các bạn trước ạ !

1: Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tạiI
Do đó; I là trực tâm
=>AI vuông góc với BC
2: Ta có: góc BAI+góc B=90 độ
góc BCE+góc B=90 độ
Do đó: góc BAI=góc BCE
3: Xét tứ giác BHCM có
BH//CM
BM//CH
Do đó: BHCM là hình bình hành
Suy ra: BH=CM và BC cắt HM tại trung điểm của mỗi đường
=>O là trng điểm của HM
hay H,O,M thẳng hàng