Một tam giác vuông cân có cạnh góc vuông bằng 5 cm . Độ dài cạnh huyền bằng ... cm ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi tam giác đó vuông cân tại A, 2 góc ở đáy là B và C
Áp dụng định lý Pytago ta có :
BC^2 = AB^2 + AC^2
hay BC^2 = 7^2 + 7^2 = 98
=> BC = \(\sqrt{98}\)
Vậy,...........

Tam giác vuông cân là tam giác vuông có 2 cạnh góc vuông bằng nhau. Gọi độ dài cạnh góc vuông là x (cm) (x > 0)
Áp dụng định lí pitago ta có:
x2 +x2 =(√2)2⇒ 2x2 = 2 => x2 =1
=> x=1cm

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
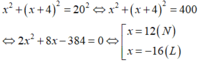
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
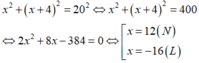
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Vì tam giác trên là tam giác vuông cân
=> Cạnh đáy bằng cạnh góc vuông
Áp dụng định lí Py - ta - go ta có :
Cạnh huyền2 = cạnh góc vuông2 + cạnh đáy2 = 22 +22 = 8
=> Cạnh huyền = \(\sqrt{8}\)(cm)

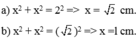

Vì một cạnh góc vuông = 5cm => cạnh góc vuông kia cũng = 5cm
Theo định lý PTG ta có: 5^2 + 5^2 = cạnh huyền^2
25 + 25 = 50
=> cạnh huyền = \(\sqrt{50}\)(cm)
Tam giác vuông cân
=> Hai cạnh góc vuông bằng nhau
Và cùng bằng 5 cm
Độ dài cạnh huyền là: \(\sqrt{5^2+5^2}=5\sqrt{2}\) (cm) (Áp dụng định lý Pytago trong tam giác vuông)