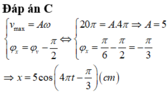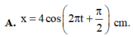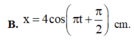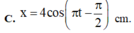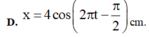Một vật dao động điều hòa với phương trình gia tốc a=-400π2cos(4πt -π/6) (cm/s). Vận tốc của vật tại thời điểm t = 19/6 là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
31 tháng 3 2019
Đáp án A
Phương pháp: a = - ω2x
Cách giải:
x (t=0,25s) = 1cm => a = - ω2x = - 40cm/s2
HT
25 tháng 7 2020
a/ \(4A=4.6=24\left(cm\right)\)
\(f=\frac{\omega}{2\pi}=\frac{4\pi}{2\pi}=2\left(Hz\right)\)
\(\varphi_0=\frac{\pi}{6}\left(rad\right)\)
b/ \(v=-\omega A\sin\left(\omega t+\varphi\right)=-4\pi.6.\sin\left(4\pi.\frac{1}{4}+\frac{\pi}{6}\right)=-4.\pi.6.\frac{-1}{2}=12\pi\left(cm/s\right)\)
\(a=-\omega.x=-4\pi.6\cos\left(4\pi.\frac{1}{4}+\frac{\pi}{6}\right)=-4\pi.6.\frac{-\sqrt{3}}{2}=12\sqrt{3}\pi\left(rad/s\right)\)
\(x=6.\cos\left(4\pi.\frac{1}{4}+\frac{\pi}{6}\right)=6.\frac{-\sqrt{3}}{2}=-3\sqrt{3}\left(cm\right)\)
d/ \(v_{max}=\omega A=4\pi.6=24\pi\left(cm/s\right)\)
\(a_{max}=\omega^2A=\left(4\pi\right)^2.6=96\pi^2\left(rad/s\right)\)
VT
29 tháng 7 2019
Đáp án C
Phương pháp: Sử dụng phương trình của li đô ̣và vâṇ tốc của chất điểm dao đông̣ điều hoà:
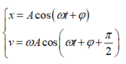
Cách giải:
- Ta có:
(chú ý bước này có thể không cần với bài này vì tất cả 4 đáp án đều có A = 5)
- Phương trình dao động của vật:
VT
30 tháng 10 2017
ü Đáp án C
+ Vận tốc cực đại của dao động amax = ωA = 4π cm/s
+ Tại thời điểm t = 0,25 vật có vận tốc
v = 2 2 v m a x = 2 π 2 cm/s
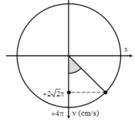
Thời điểm t = 0 ứng với góc lùi Δφ = ωΔt = 0,25π.
Biểu diễn các vị trí tương ứng trên đường tròn. Ta thu được: φ 0 = - π 2 rad.
+ Phương trình dao động của vật
x = 4 cos π t - π 2 cm.
VT
21 tháng 5 2017
Phương trình:
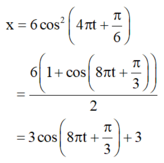
- Mà t = 0,125 = T/2 nên S = 2.3 = 6 cm
Chọn đáp án A
VT
2 tháng 7 2018
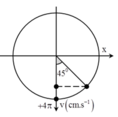
+ Vận tốc cực đại của dao động amax = ωA = 4π cm/s.
+ Tại thời điểm t = 0,25 vật có vận tốc
v = 2 2 v m a x = 2 π 2 cm/s
Thời điểm t = 0 ứng với góc lùi Δφ = ωΔt = 0,25π.
Biểu diễn các vị trí tương ứng trên đường tròn. Ta thu được: φ 0 = - π 2 rad
+ Phương trình dao động của vật
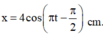
Đáp án C
