Tam giác ABC vuông tại A,AB=a,AC=3a.Trên cạnh AC lấy các điểm D,E sao cho AD=DE=EC
a.Chứng minh \(\dfrac{DE}{DB}=\dfrac{DB}{DC}\)
b.Chứng minh tam giác BDE đồng dạng với tam giác CDB
c.Tính tổng góc AEB+góc BCD
GIÚP MÌNH LÀM BÀI NÀY TRƯỚC T2 NHÉ CÁC BẠN!:)))))))))))))))))))))))))))CẢM ƠN CÁC BẠN NHIỀU LẮM!:)))))))))))))))))))))))))))))))

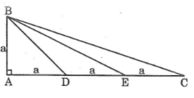

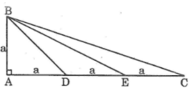


a: \(\dfrac{DE}{DB}=\dfrac{a}{a\sqrt{2}}\)
\(\dfrac{DB}{DC}=\dfrac{a}{a\sqrt{2}}\)
Do đó: DE/DB=DB/DC
b: Xét ΔBDE và ΔCDB có
DB/DC=DE/DB
góc BDE=góc CDB
Do đó: ΔBDE đồng dạng với ΔCDB