trên 1 đường thẳng AB dài 120km, xe thứ nhất đi từ A đến B, cứ sau 15p chuyển động thẳng đều, ô tô dừng nghỉ 5 p. Trong khoảng thời gian 15p đầu vận tốc của xe thứ nhất là v1=10km/h 15p thứ 2 xe đi với vận tốc 2v1 , 15 phút thứ 3 xe đi với vận tốc 3v1,... cứ thế đến B tính vận tốc trung bình trên quãng đường AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
7 tháng 8 2016
bài 4:
Giải :
a.Sau khi tăng tốc thêm 3 km/h thì đến nơi sớm hơn dự kiến là 1h ,mà S là như nhau nên theo bài ra ta có:
V1.t = (V1 +3 ).(t -1).
12.t = (12+3 ).(t -1).
12.t = 15.t -15.
15 = 15.t – 12.t.
5 = t.
b. Gọi t’1 là thời gian đi quãng đường s1: t’1 = S1/V1 ( / : là chia).
Thời gian sửa xe : t = 15 phút = ¼ h.
Thời gian đi quãng đường còn lại : t’2 = (S1-S2)/V2.
Theo bài ra ta có : t1 – (t’1 + ¼ + t’2) = 30 ph = ½ h.
T1 – S1/V1 – ¼ - (S-S1)/V2 = ½. (1).
S/V1 – S/V2 – S1.(1/V1- 1/V2) = ½ +1 /4 =3/4 (2).
Từ (1) và (2) suy ra: S1.(1/V1 – 1/V2) = 1- ¾ = ¼.
Hay S1 = ¼ . (V1- V2)/(V2-V1) = ¼ . (12.15)/(15-12) = 15 km.
TN
7 tháng 8 2016
bài 1:
a) Lúc xe từ B xuất phat thì xxe từ A đi được quáng đường: S=40 km
*/PTCĐ:
X1= 40+ 40*t
X2= 25*t
VT
25 tháng 10 2019
Đáp án B
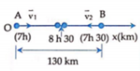
Chọn trục Ox trùng với đường AB, gốc O tại A, chiều dương hướng từ A sang B. Gốc thời gian là lúc 7 giờ . Sau thời gian t >0,5h;
- Toạ độ của xe thứ nhất: 
- Toạ độ của xe thứ hai: 
Khi hai xe gặp nhau lúc 8 giờ 30 phút hay t=1,5h
(Dễ thấy với t <0,5h xe thứ nhất không thể gặp xe thứ hai)
18 tháng 6 2016
khi người 3 xuất phát thì người 1 cách A là (0,5+0,25).8=6(km)
2 cách A là 0,5.12 =6(km)
gọi C là nơi nguời 1 gặp người 3
thời gian người 1 gặp người 3 là t=6V3−8
khi đó người 2 cách hai người kia là S=(12−8).6V3−8
=24V3−8
Do sau 30 phut từ khi gặp người 1 người 3 cách đều 2 người kia ta có phương trình
(V3−8).0,5=S+(12−V3).0,5 từ đó tìm được V3
Bài làm:
Xét quãng đường AB, ta có:
AB = s1 + s2 + ... + CB
⇔ AB = v1.t + v2.t + ... + vn.t + CB (1)
⇔ 120 = 10.0,25 + 2.2,5 + ... + n.2,5 + CB (2)
⇔ 120 = 2,5.(1 + 2 + ... + n) + CB
⇔ 120 = 2,5.\(\dfrac{n\left(n+1\right)}{2}\) + CB
⇔ 120 = 1,25.n(n + 1) + CB (*)
⇔ 1,25.n(n + 1) < 120
⇔ n(n + 1) < 96
⇒ n = 9.
Thay n = 9 vào (*) ⇒ CB = 120 - 1,25.90 = 7,5(km)
Thời gian đi hết quãng đường AB là:
tAB = 9.0,25 + 9.\(\dfrac{5}{60}\) + tCB
tCB = \(\dfrac{10}{v_{CB}}\) = \(\dfrac{10}{v_{10}}\) = \(\dfrac{10}{10.10}\) = \(\dfrac{10}{100}\) = 0,1(giờ)
⇒ tAB = 9.0,25 + 9.\(\dfrac{5}{60}\) + 0,1 = 3,1(giờ)
Vận tốc trung bình trên quãng đường AB là:
vtb = \(\dfrac{s_{AB}}{t}\) = \(\dfrac{120}{3,1}\) = \(\dfrac{1200}{31}\)(km/h)
Vậy vận tốc trung bình trên quãng đường AB là \(\dfrac{1200}{31}\) km/h.
Giải thích cách chuyển từ (1) thành (2):
Ta có: s1 = v1.t = 10.0,25 = 2,5(km)
s2 = v2.t = 2v1.t = 2.2,5(km)
Rồi tương tự như vậy cho đến n.
(Copy bài nhớ ghi rõ nguồn copy nhé!)
pn quên chưa ghi nguồn!!!