Cho đoạn thẳng AB = 2^2001. Gọi M1 là trung điểm của đoạn thẳng AB , M2 là trung điểm của đoạn thẳng AM1, M3 là trung điểm của đoạn thẳng AM2 ,.............., M2011 là trung điểm của đoạn thẳng AM2010. Tính độ dài đoạn thẳng AM2010, AM2011
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2016
a)
Vì M1 là trung điểm của đoạn thẳng AB => M1 nằm giữa hai điểm A và B (1) Vì M2 là trung điểm của đoạn thẳng M1B => M2 nằm giữa hai điểm M1 và B (2) Từ (1), (2) => M1 nằm giữa A và M2 Độ dài đoạn thẳng M1B là: M1B = AM1 = AB/2 = a/2 = 1/2 a Độ dài đoạn thẳng M2B là: M2B = M1M2 = M1B/2 = 1/2 . a/2 = 1/22 a Vì M1 nằm giữa A và M2B AM2 = AM1 + M1M2 = 1/2 a + 1/2² a = 3/4 a b) M1B = 1/2 a M2B = 1/2² a Độ dài đoạn thẳng M3B là: M3B = M2B/2 = 1/2³ a Tương tự Độ dài đoạn thẳng M8B là: M8B = M7B/2 = 1/28 a Vì M1, M2, M3,... lần lượt nằm giữa các điểm A và B, M1 và B, M2 và B, .... => M8 nằm giữa A và B => AB = AM8 + M8B => AM8 = AB — M8B = a — 1/28a = 255/256 a
12 tháng 2 2016
xét 2 trường hợp ban nhe
kết quả là 1021 mình chắc chắn với bạn đó
DD
Đoàn Đức Hà
Giáo viên
9 tháng 8 2021
\(A=AM_1+AM_2+AM_3+...+AM_{2020}\)
\(=\frac{1}{2^1}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{2020}}\)
\(2A=1+\frac{1}{2^1}+\frac{1}{2^2}+...+\frac{1}{2^{2019}}\)
\(2A-A=\left(1+\frac{1}{2^1}+\frac{1}{2^2}+...+\frac{1}{2^{2019}}\right)-\left(\frac{1}{2^1}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{2020}}\right)\)
\(A=1-\frac{1}{2^{2020}}< 1=AB\)
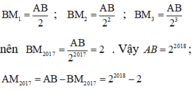
Chúc bạn học tốt
Ko trả lời thì thôi chúc làm gì ?