hàm số y=(x2 -4)2 . (1-2x)3 có bao nhiêu điểm cực trị
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 8 2018
Đáp án B
Phương pháp: Đạo hàm của hàm hợp : 
Tìm số nghiệm của phương trình y’ = f’(x2 – 2x) = 0
Cách giải:
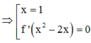
Vì f(x) liên tục trên R và có đúng ba điểm cực trị là –2; –1; 0 nên f’(x) đổi dấu tại đúng ba điểm –2; –1; 0 và f’(–2) = f’(–1) = f(0) = 0
Giải các phương trình:
: vô nghiệm
Như vậy, y’ = 0 có 3 nghiệm x = 0;1;2 và y’ đều đổi dấu tại 3 điểm này. Do đó, hàm số y = f(x2 – 2x) có 3 điểm cực trị
CM
28 tháng 11 2019
Đáp án D
f ' ( x ) = 0 ⇔ ( x - 1 ) 2017 ( x 2 - 1 ) ( 2 x + 3 ) 3 = 0 ⇔ x = 1 x = - 1 x = - 3 2
Xét dấu:
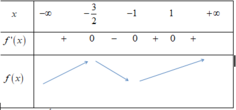
Vậy hàm số có 2 cực trị
CM
26 tháng 6 2019
Đáp án A.
Đặt u = x 2 - 2 x , ta có y = f u ⇒ y ' = 2 x - 2 f ' u = 2 x - 2 f ' x 2 - 2 x .
Do đó, phương trình y ' = 0 ⇔ [ 2 x - 2 = 0 x 2 - 2 x = - 2 x 2 - 2 x = - 1 x 2 - 2 x = 0 ⇔ [ x - 1 3 = 0 x 2 - 2 x + 2 = 0 x 2 - 2 x = 0 ⇔ [ x = 0 x = 1 x = 2 .
Vậy hàm số đã chốc 3 điểm cực trị là x = 0; x= 1; x = 2.
\(y'=4x\left(x^2-4\right)\left(1-2x\right)^3-6\left(1-2x\right)^2\left(x^2-4\right)^2\)
\(=2\left(x^2-4\right)\left(1-2x\right)^2\left[2x\left(1-2x\right)-3\left(x^2-4\right)\right]\)
\(=2\left(x^2-4\right)\left(1-2x\right)^2\left(-7x^2+2x+12\right)\)
\(y'=0\) có 4 nghiệm bội lẻ \(\Rightarrow\) hàm có 4 cực trị