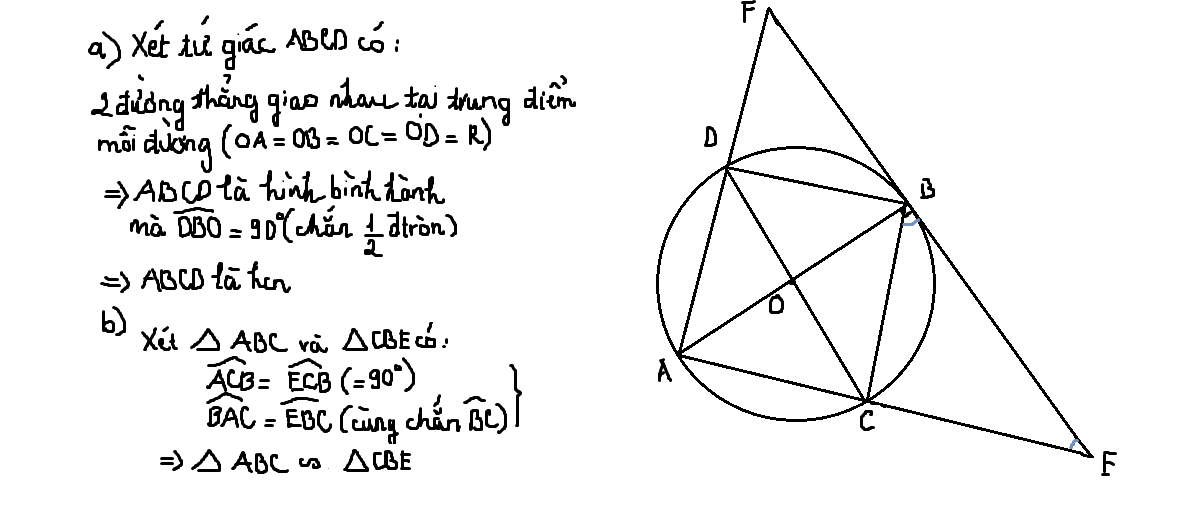
Cho đường tròn đường kính AB, d tiếp xúc (O) tại A. Dựng đường kính MN khác AB, các đường thẳng BM, BN cắt d tại E, F
a,Chứng minh AMBN là hình chữ nhật
b,Chứng minh MN tiếp xúc với đường tròn đường kính AE, AF
c, Chứng minh AE.AF ko đổi
d, Tìm vị trí MN để EF min ,diện tích MENF min , ME + NF nhỏ nhất