Giải giùm em câu 2.1b, thanks nhiều ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TG
1
21 tháng 12 2021
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-2x-3=-\dfrac{1}{2}x+3\\y=-2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{3}{2}x=6\\y=-2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=8-3=5\end{matrix}\right.\)
8 tháng 7 2018
không nhé
(2x+1)(4x^2-xy+1)-(8x^3-1)
= ((2x)^3 -1) - ( 8x^3 - 1 ) = 0
Vậy là không phụ thuộc vào biến nhé bạn
S
27 tháng 11 2021
để em viết ra vậy ạ
cho tam giac mnp vuông tại m (mn>mp) có đường cao mk
a) biết mn=20cm, mp=15cm, tính mk và góc mnp (góc làm tròn đến đơn vị phút).
b) vẽ trung tuyến me của tam giác mnp. từ p vẽ đường thẳng vuông góc với me cắt mn tại d. cm tam giác mnp đồng dạng với tam giác mpd, từ đó suy ra mn.md=np.pk
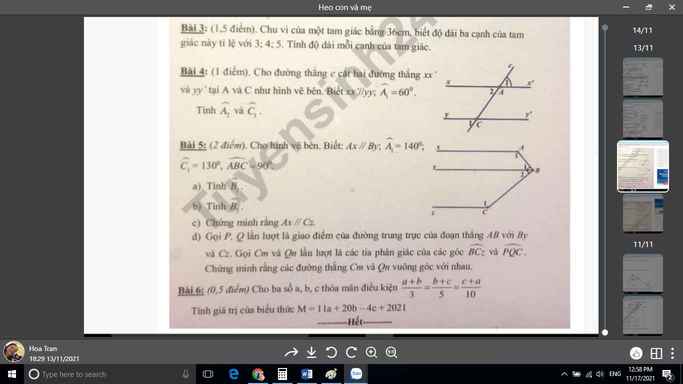
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
Bạn không chụp hết đề nhưng mình đoán là tìm $m$ để hàm số đồng biến trên $\mathbb{R}$
Lời giải:
Để hàm số đồng biến trên $\mathbb{R}$ thì:
$y'=3mx^2-2(2m-1)x+(m-2)\geq 0, \forall x\in\mathbb{R}$
Điều này xảy ra khi:
\(\left\{\begin{matrix} 3m>0\\ \Delta'=(2m-1)^2-3m(m-2)\leq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>0\\ (m+1)^2\leq 0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m>0\\ m=-1\end{matrix}\right.\) (vô lý)
Vậy không tồn tại $m$ để hs đồng biến trên $\mathbb{R}$