Giải BPT
x6 - 14x4 + 49x2 > 36
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BPT\(\Leftrightarrow\left|x^2+3x+2\right|>2x-x^2\)
TH1:\(2x-x^2< 0\Leftrightarrow x\in R\backslash\left[0;2\right]\) (1)
TH2:\(\left\{{}\begin{matrix}2x-x^2\ge0\\\left(x^2+3x+2\right)^2>\left(2x-x^2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\in\left[0;2\right]\\\left(2x^2+x+2\right)\left(5x+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\in\left[0;2\right]\\5x+2>0\end{matrix}\right.\)\(\Rightarrow x\in\left[0;2\right]\) (2)
Từ (1) (2) suy ra \(x\in R\)

ĐKXĐ: \(x\ge2\)
BĐT trở thành:
\(x+\sqrt{x-2}\le2+\sqrt{x-2}\Rightarrow x\le2\)
Kết hợp điều kiện ban đầu ta được: \(x=2\)
Vậy BPT có nghiệm duy nhất \(x=2\)



Đề bài thiếu bạn, BPT thiếu 1 vế, vế còn lại là \(\ge0;\le0,>0,< 0\)?


Điều kiện xác định : \(2x^2-3x-5\ge0\Leftrightarrow\left(x+1\right)\left(2x-5\right)\ge0\Leftrightarrow\orbr{\begin{cases}x\ge\frac{5}{2}\\x\le-1\end{cases}}\)
Ta có : \(1-x+2\sqrt{2x^2-3x-5}< 0\Leftrightarrow2\sqrt{2x^2-3x-5}< x-1\)
Bình phương hai vế : \(4\left(2x^2-3x-5\right)< x^2-2x+1\)
\(\Leftrightarrow7x^2-10x-21< 0\)
Tới đây lập bảng xét dấu là ra nhé :)
(Cần chú ý tới điều kiện của bài toán)
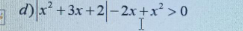 Giải bpt sau :
Giải bpt sau :
\(x^6-14x^4+49x^2>36\)
\(\Leftrightarrow x^6-x^5+x^5-x^4-13x^4+13x^3-13x^3+13x^2+36x^2-36x+36x-36>0\)
\(\Leftrightarrow x^5\left(x-1\right)+x^4\left(x-1\right)-13x^3\left(x-1\right)-13x^2\left(x-1\right)+36x\left(x-1\right)+36\left(x-1\right)>0\)
\(\Leftrightarrow\left(x-1\right)\left(x^5+x^4-13x^3-13x^2+36x+36\right)>0\)
\(\Leftrightarrow\left(x-1\right)\left[x^4\left(x+1\right)-13x^2\left(x+1\right)+36\left(x+1\right)\right]>0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x^4-13x^2+36\right)>0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x^4-9x^2-4x^2+36\right)>0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left[x^2\left(x^2-9\right)-4\left(x^2-9\right)\right]>0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x^2-9\right)\left(x^2-4\right) >0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\left(x+3\right)\left(x-3\right)>0\)
Để \(\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\left(x+3\right)\left(x-3\right)>0\)
\(\Rightarrow\left[{}\begin{matrix}x>3\\x< -3\end{matrix}\right.\)
Vậy để \(\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\left(x+3\right)\left(x-3\right)>0\) thì x>3 hoặc x<-3