chứng minh rằng trong một đường tròn hai cung bị chắn giữa hai giây bằng nhau
2 trường hợp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 10 2017
Vẽ đường tròn tâm O, các dây cung AB // CD.
Cần chứng minh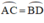 
Cách 1:
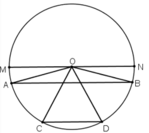
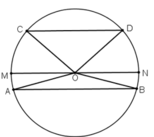
Kẻ bán kính MN // AB // CD
MN // AB
+ TH1: AB và CD cùng nằm trong một nửa đường tròn.
.
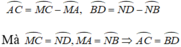+ TH2: AB và CD thuộc hai nửa đường tròn khác nhau.
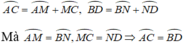
Cách 2:
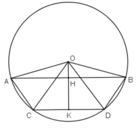
Kẻ OH ⊥ AB; OK ⊥ CD (H ∈ AB, K ∈ CD)
Vì AB // CD ⇒ O, H, K thẳng hàng.
ΔOAB có OA = OB
⇒ ΔOAB cân tại O
⇒ đường cao OH đồng thời là đường phân giác
⇒ 
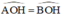
Chứng minh tương tự:
CM
21 tháng 11 2018
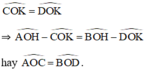
Vẽ đường tròn tâm O, các dây cung AB // CD.
Cần chứng minh AC ^ = BD ^
Cách 1:
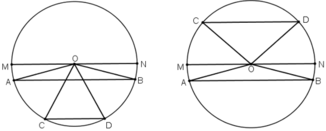
Kẻ bán kính MN // AB // CD
MN // AB
+ TH1: AB và CD cùng nằm trong một nửa đường tròn.
.
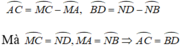+ TH2: AB và CD thuộc hai nửa đường tròn khác nhau.
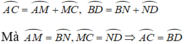
Cách 2:
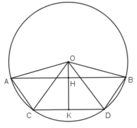
Kẻ OH ⊥ AB; OK ⊥ CD (H ∈ AB, K ∈ CD)
Vì AB // CD ⇒ O, H, K thẳng hàng.
ΔOAB có OA = OB
⇒ ΔOAB cân tại O
⇒ đường cao OH đồng thời là đường phân giác
⇒ 
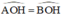
Chứng minh tương tự:
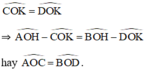
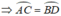
Kiến thức áp dụng
+ Trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.
+ Trong cùng một đường tròn, hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau, tức là góc ở tâm chắn hai cung đó bằng nhau.
QD
11 tháng 4 2017
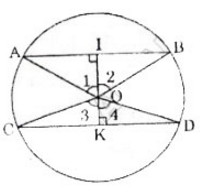
Giả sử AB và CD là các dây song song của đường tròn (O).
Kẻ OI ⊥ AB (I ∈ AB) và OK ⊥ CD (K∈CD).
Do AB //CD nên I,O,K thẳng hàng.
Do các tamgiác OAB, OCD là các tam giác cân đỉnh O nên các đường cao kẻ từ đỉnh đồng thời là phân giác.
Vì vậy ta có: Góc ∠O1 = ∠O2, ∠O3 = ∠O4
Giả sử AB nằm ngoài góc COD, ta có: ∠AOC = 1800 – (∠O1 + ∠O3) = 1800 -(∠O2 + ∠O4) = ∠BOD
Suy ra cung AC= cung BD.
Nghĩa là hai cung bị chắn giữa hai dây song song thì bằng nhau. Các trường hợp khác ta chứng minh tương tự.
TA
12 tháng 1 2018
Bài này có 2 TH, ta phải xét cả 2 TH (vì ko có ghi rõ đề):
TH 1:
Xét Δ
AOB có:
OA = OB (cùng bán kính)
Do đó: Δ
AOB cân tại A
⇒
ˆOAB=ˆOBA
Ta có: ˆAOM=ˆOBA
(2 góc so le trong do AB//MN)
ˆNOB=ˆOBA
( // )
mà ˆOAB=ˆOBA
(cmt)
⇒
ˆMOA=ˆNOB
(1)
CM tương tự, ta được: ˆMOC=ˆNOD
(2)
Từ (1) và (2) suy ra \(\widehat{AOC}=\widehat{BOD}\)
⇒ \(\widebat{AC}=\widebat{BD}\)
TH 2 :
CM y như câu a) (mà chỉ thay đổi cách CM \(\widehat{AOC}=\widehat{BOD}\) )
HQ
2
NT
29 tháng 1 2016
Gọi đường tròn Ở, 2 dây AB ss với CD
xet Tu giac ABCD co AD=AO+OD
CB=CO+OB
mà CO=OB=OA=OD
=> tu giac ABCD là hinh chu nhat
=>AOB=COD
=>cung CD=cungAB
CM
18 tháng 11 2017
(A) Sai. Góc nội tiếp là góc có đỉnh nằm trên đường tròn, hai cạnh chứa hai dây cung của đường tròn đó.
(B) Sai. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung hoặc chắn hai cung bằng nhau.
(C) Sai. Trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau.
(D) Sai. Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của góc ở tâm cùng chắn một cung.
(E) Đúng. Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
HH
19 tháng 1 2021
Kẻ \(OH\perp AB;OK\perp CD\left(H\in AB,K\in CD\right)\)
Vì AB // CD => O, H, K thẳng hàng.
Tam giác OAB có OA = OB
=> Tam giác OAB cân tại O
=> Đường cao OH đồng thời là đường phân giác
=> ^AOH = ^BOH
Chứng minh tương tự , ta có :
^COK = ^DOK
=> ^AOH - ^COK = ^BOH - ^DOK
hay ^AOC = ^BOD
\(\Rightarrow\widebat{AC}=\widebat{BD}\)
11 tháng 4 2017
a) Nối C đến D.
Ta có 2 đường tròn bằng nhau => AC = AD
=> ∆ ACD cân tại A
Lại có góc ABC = 90°; do có OB = OC = OA = R ( tính chất trung tuyến ứng với cạnh huyền )
Tương tự có góc ABD = 90°
=> ABC + ABD = 180°
=> C; B; D thẳng hàng và AB ⊥ CD
=> BC = BD
=> cung BC = cung BD
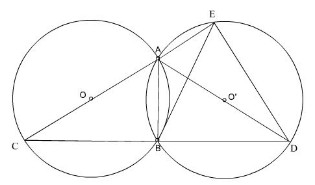
b) Nối E đến D; từ B hạ BH ⊥ ED Ta có góc DEA = 90° ( chứng minh tương tự theo (a) )
=> BH // EC
Mà theo (a) ta có BE = BD
=> BH là đường trung bình tam giác CDE
=> HE = HD mà BH ⊥ ED => B là điểm chính giữa cung EBD
