Tìm nghiệm của 2x4 + 4x3 - 16x + 16
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D
B = lim x → 2 x 4 − 5 x 2 + 4 x 3 − 8 = lim x → 2 ( x 2 − 1 ) ( x 2 − 4 ) x 3 − 2 3
= lim x → 2 ( x 2 − 1 ) ( x − 2 ) ( x + 2 ) ( x − 2 ) ( x 2 + 2 x + 4 )
= lim x → 2 ( x 2 − 1 ) ( x + 2 ) x 2 + 2 x + 4 = ( 2 2 − 1 ) . ( 2 + 2 ) 2 2 + 2.2 + 4 = 1

Ta có x 4 – 4 x 3 + 8 x 2 – 16 x + 16 = 0 ⇔ ( x 4 + 8 x 2 + 16 ) – ( 4 x 3 + 16 x ) = 0 ⇔ x 2 + 4 2 - 4 x x 2 + 4 = 0 ⇔ x 2 + 4 x 2 + 4 - 4 x = 0 ⇔ x 2 + 4 x - 2 2 = 0

ó x = 2
Vậy x 0 = 2
Đáp án cần chọn là: B


a) \(P\left(x\right)=3x^3-x^2-2x^4+3+2x^3+x+3x^4-x^2-2x^4+3+2x^3+x+3x^4\)
\(=2x^4+7x^3-2x^2+2x+6\)
\(Q\left(x\right)=-x^4+x^2-4x^3-2+2x^2-x-x^3-x^4+x^2-4x^3-2+2x^2-x-x^3\)
\(=-2x^4-10x^3+6x^2-2x-4\)
b) \(P\left(x\right)+Q\left(x\right)=2x^4+7x^3-2x^2+2x+6-2x^4-10x^3+6x^2-2x-4\)
\(=-3x^3+4x^2+2\)

Ta có: \(5x^2+2xy+y^2-16x+16=0\)
\(\Leftrightarrow\left(4x^2-16x+16\right)+\left(x^2+2xy+y^2\right)=0\)
\(\Leftrightarrow4\left(x-2\right)^2+\left(x+y\right)^2=0\)
Vì \(\hept{\begin{cases}4\left(x-2\right)^2\ge0;\forall x,y\\\left(x+y\right)^2\ge0;\forall x,y\end{cases}}\)\(\Rightarrow4\left(x-2\right)^2+\left(x+y\right)^2\ge0;\forall x,y\)
Do đó \(4\left(x-2\right)^2+\left(x+y\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}4\left(x-2\right)^2=0\\\left(x+y\right)^2=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\y=-2\end{cases}}\)
Vậy ...
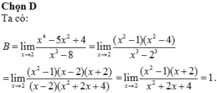

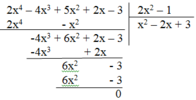
2x4 + 4x3 - 16x + 16
Vì:
+) x4 > 0 ∀ x ∈ R
+) x3 > 0 ∀ x ∈ R
=> 2x4 + 4x3 - 16x + 16 > 0 ∀ x ∈ R.
Vậy 2x4 + 4x3 - 16x + 16 không có nghiệm.
Chúc bạn học tốt!