Đặt một hiệu điện thế U=3,2V vào 2 đầu điện trở có R_1=20Ω
a Tính cường độ dòng điện I_1 đi qua điện trở này.
b Giữ nguyên hiệu điện thế U đã cho trên đây, thay điện trở R_1 bằng điện trở R_2 sao cho dòng điện qua R_2 có cường độ I_2=0,8I_1. TínhR_2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1 tháng 3 2017
Ta có : I 2 = 0,8 I 1 = 0,8 × 0,16 = 0,128A.
⇒ Điện trở qua
R
2
là: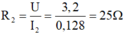 
HK
9 tháng 7 2022
Ta có : I 2 = 0,8 I 1 = 0,8 × 0,16 = 0,128A.
⇒ Điện trở qua R 2 là:
R2= U/I2= 3,2/0,128 =25 \(\Omega\)
13 tháng 10 2021
a) Cường độ dòng điện:
\(I_1=\dfrac{U}{R_1}=\dfrac{12}{6}=2\left(A\right)\)
b) Ta có: \(I_2=\dfrac{I_1}{2}=\dfrac{2}{2}=1\left(A\right)\)
Giá trị R2: \(R_2=\dfrac{U}{I_2}=\dfrac{12}{1}=12\left(\Omega\right)\)
N
12 tháng 10 2021
Bạn tự làm tóm tắt nhé!
Cường độ dòng điện: \(I=\dfrac{U}{R}=\dfrac{12}{6}=2A\)
\(U=U_{2_{ }}=12V\left(gt\right)\)
\(I_2=2.\dfrac{1}{2}=1A\)
Giá trị của R2: \(R_2=\dfrac{U2}{I2}=\dfrac{12}{1}=12\Omega\)
12 tháng 10 2021
a) Cường độ dòng điện:
\(I_1=\dfrac{U}{R}=\dfrac{12}{6}=2\left(A\right)\)
b) Ta có: \(I_2=\dfrac{I_1}{2}=\dfrac{2}{2}=1\left(A\right)\)
Gía trị R2:
\(R_2=\dfrac{U_2}{I_2}=\dfrac{12}{1}=12\left(\Omega\right)\)
16 tháng 9 2021
Ta có: \(\dfrac{I}{I'}=\dfrac{\dfrac{U}{R}}{\dfrac{U}{R'}}=\dfrac{R'}{R}=\dfrac{2R}{R}=2\Rightarrow I'=\dfrac{I}{2}=\dfrac{0,2}{2}=0,1\left(A\right)\)
Ta có: \(\dfrac{I}{I"}=\dfrac{U}{U"}=\dfrac{U}{3U}=\dfrac{1}{3}\Rightarrow I'=\dfrac{I}{\dfrac{1}{3}}=\dfrac{0,2}{\dfrac{1}{3}}=0,6\left(A\right)\)
22 tháng 7 2018
Tóm tắt :
\(R_1=2R_2\)
\(U=16V\)
\(R_1//R_2\)
\(I_2=I_1+6\)
\(R_1;R_2=?\)
\(I_1;I_2=?\)
GIẢI :
Vì R1//R2 nên :
\(U=U_1=U_2=16V\)
Cường độ dòng điện qua R1 là :
\(I_1=\dfrac{U}{R_1}\)
Cường độ dòng điện qua R2 là :
\(I_2=\dfrac{U}{R_2}\)
Ta có : \(\dfrac{I_1}{I_2}=\dfrac{R_2}{R_1}\) (I và R là 2 đại lượng tỉ lệ nghịch)
Theo đề có : R1 = 4R2
Suy ra : \(\dfrac{R_2}{R_1}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{I_1}{I_2}=\dfrac{1}{4}=>4I_1=I_2\) (1)
Và : \(I_2=I_1+6\) (2)
Ta thay 4I1 ở (1) vào biểu thức chứa I2 ở (2) có :
\(4I_1=I_1+6\)
\(\Rightarrow I_1=\dfrac{6}{3}=2\left(A\right)\)
\(\Rightarrow I_2=I_1+6=2+6=8\left(A\right)\)
Điện trở R1 là :
\(U=I_1.R_1=>R_1=\dfrac{U}{I_1}=\dfrac{16}{2}=8\left(\Omega\right)\)
Điện trở R2 là :
\(U=I_2.R_2=>R_2=\dfrac{U}{I_2}=\dfrac{16}{8}=2\left(\Omega\right)\)
Vậy : \(\left\{{}\begin{matrix}R_1=8\Omega\\R_2=2\Omega\\I_1=2A\\I_2=8A\end{matrix}\right.\)
T
22 tháng 7 2018
Vì I1=I1 và I2=I1+6 nên không thể mắc nối tiếp hai điện trở này
=> R1//R2
=> Vì R1//R2=>U1=U2=U=16V
=> I1=\(\dfrac{U1}{R1}=\dfrac{16}{4R2}=\dfrac{4}{R2}\)
=>I2=\(\dfrac{U2}{R2}=\dfrac{16}{R2}\)
Mặt khác ta có I2=I1+6=>\(\dfrac{16}{R2}=\dfrac{4}{R2}+6=>R2=2\Omega;R1=8\Omega\)
Vậy..........
23 tháng 5 2022
\(R_{tđ}=R_1+R_2+\dfrac{U}{I}=40\Omega\)
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{U}{I'}=7,5\Omega\)
Giải theo hệ PT theo \(R_1;R_2\) ta được: \(R_1=30\Omega;R_2=10\Omega\)
Hoặc: \(R_1=10\Omega;R_2=30\Omega\)
23 tháng 5 2022
a, Cường độ tương đương của mạch:
\(R_{tđ}=R_1+R_2=40\Omega\)
Cường độ dòng điện qua mỗi điện trở:
\(I=\dfrac{U}{R_1+R_2}=\dfrac{12}{25+15}=0,3A\)
b, Đổi \(S=0,06mm^2=0,06.10^{-6}m^2\)
Công thức tính điện trở:
\(R=\rho\dfrac{\iota}{S}\Rightarrow l=\dfrac{RS}{\rho}\)
Thay số vào: \(\left(15.0,06.10^{-6}\right)/0,5.10^{-6}=\dfrac{9}{5}=1.8m\)
23 tháng 5 2022
a)Điện trở tương đương trong mạch: \(R=R_1+R_2=25+15=40\Omega\)
Dòng điện qua mạch: \(I=\dfrac{U}{R}=\dfrac{12}{40}=0,3A\)
Hai điện trở mắc nối tiếp\(\Rightarrow I_{R1}=I_{R2}=I_{mạch}=0,3A\)
b)Chiều dài dây dẫn:
\(R=\rho\dfrac{l}{S}\Rightarrow l=\dfrac{R\cdot S}{\rho}=\dfrac{15\cdot0,06\cdot10^{-6}}{0,5\cdot10^{-6}}=1,8m\)
21 tháng 8 2016
ta có:
do I tỉ lệ nghịch với điện trở nên I=2I'=0,1A
do U tỉ lệ thuận với cường độ dòng điện nên I'''=3I=0,6A
a,\(\Rightarrow I1=\dfrac{U}{R1}=\dfrac{3,2}{20}=0,16A\)
b,\(\Rightarrow R2=\dfrac{U}{I2}=\dfrac{3,2}{0,8I1}=\dfrac{3,2}{0,8.0,16}=25\Omega\)