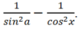Rút gọn biểu thức: cota+ tana/ 1+ tan2a.tana
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 9 2019
Chọn C.
Ta có: cota + tana) 2 = cot2a + 2.cota.tana + tan2a
= (cot2a + 1) + (tan2a + 1)
PT
1
CD
27 tháng 4 2020
Ta có : \(\sin^2a+\cos^2a=1\Rightarrow\cos a=\frac{\sqrt{21}}{5}\)
Ta có : \(\frac{\cot a-\tan a}{\cot a+\tan a}=\frac{\frac{\cos a}{\sin a}-\frac{\sin a}{\cos a}}{\frac{\cos a}{\sin a}+\frac{\sin a}{\cos a}}\\ =\frac{\frac{\frac{\sqrt{21}}{5}}{\frac{2}{5}}-\frac{\frac{2}{5}}{\frac{\sqrt{21}}{5}}}{\frac{\frac{\sqrt{21}}{5}}{\frac{2}{5}}+\frac{\frac{2}{5}}{\frac{\sqrt{21}}{5}}}=\frac{17}{25}=0,68\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 6 2020
\(-\frac{\pi}{2}< a< 0\Rightarrow cosa>0\)
\(\Rightarrow cosa=\sqrt{1-sin^2a}=\frac{4}{5}\)
\(tana=\frac{sina}{cosa}=-\frac{3}{4}\)
\(A=\frac{tana+cota}{1+tan^2a}=\frac{tana+\frac{1}{tana}}{1+tan^2a}=\frac{1+tan^2a}{\left(1+tan^2a\right)tana}=\frac{1}{tana}=cota\)
TN
0
NT
0
